标签:while 0-1背包 turn cap 价值 inf 情况下 关于 树形结构
利用回溯算法求解八皇后问题
八皇后问题(eight queens problem)是国际西洋棋棋手马克斯·贝瑟尔于1848年提出:在8×8格的国际象棋上摆放八个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法。可以把8皇后问题扩展到n皇后问题,即在nxn的棋盘上摆放n个皇后,使任意两个皇后都不能处于同一行、同一列或同一斜线上。
回溯法设计思路
回溯法从解空间树的根节点出发,按照深度优先策略搜索满足约束条件的解。在搜索至树中节点时,先判断该节点对应的部分解是否满足条件,也就是判断该节点是否包含问题的(最优)解,如果肯定不包含,则跳过以该节点为根的子树,即所谓剪枝。否则进入以该节点给根的子树,继续按照深度优先策略进行搜索。
#include <iostream>
#include<math.h>
using namespace std;
int Place(int k,int x[])
{
for(int i=0;i<k;i++)
if(x[i]==x[k] || abs(i-k)==abs(x[i]-x[k]))
return 1;
return 0;
}
int Queen(int n,int x[],int sum)
{
int k=0;
int flag=0;//有无解标志
while (k>=0)
{
x[k]++;
while(x[k]<n && Place(k,x)==1)
x[k]++;
if(x[k]<n && k==n-1)
{
flag=1;//有解
sum++;
for(int i=0;i<n;i++)
cout<<x[i]+1<<" ";
cout<<endl;
if(k<n && x[0]<n)
{
x[k--]=-1;//回溯
continue;
}
}
if(x[k]<n && k<n-1)
k+=1;
else
x[k--]=-1;
}
if(flag==0)
cout<<"无解。"<<endl;
return sum;
}
int main()
{
int sum=0;
int n=8;//皇后个数
int x[8];
for(int i=0;i<n;i++)
x[i]=-1;
sum=Queen(n,x,sum);
cout<<"解毕,共有 "<< sum <<" 个解。"<<endl;
return 0;
}
#include<iostream>
using namespace std;
int Capacity; //背包容量
bool selected[10000]; //当前选择方案
bool optimal[10000]; //最佳选择方案
int maxTotalValue = 0; //最大价值
int valueofPackage = 0; //当前背包价值
int residualCapacity; //剩余背包价值
int n;
int weight[10000]; //背包重量
int value[10000]; //背包价值
void dfs(int i)
{
if(i > n){
if(valueofPackage >= maxTotalValue){
for(int i = 1 ; i <= n ; i++){
optimal[i] = selected[i];
}
maxTotalValue = valueofPackage;
}
return;
}else{
residualCapacity -= weight[i];
if(residualCapacity >= 0){ //遍历左子树
selected[i] = 1;
valueofPackage += value[i];
dfs(i+1);
selected[i] = 0;
valueofPackage -= value[i];
residualCapacity += weight[i];
}else{//不满足原路返回
residualCapacity += weight[i];
}
}
//遍历右子树
dfs(i+1);
}
int main(){
cout<<"输入背包容量:"<<endl;
cin>>Capacity;
residualCapacity = Capacity;
cout<<"请输入背包个数:"<<endl;
cin>>n;
cout<<"请输入每个背包重量:"<<endl;
for(int i = 1 ; i <= n ; i++){
cin>>weight[i];
}
cout<<"请输入每个背包价值:"<<endl;
for(int i = 1 ; i <= n ; i++){
cin>>value[i];
}
dfs(1);
cout<<"最佳方案为:"<<endl;
for(int i = 1 ; i <= n ; i++){
if(optimal[i] == 1){
cout<<i<<" ";
}
}
cout<<endl<<"最大背包价值为:"<<endl<<maxTotalValue;
return 0;
}
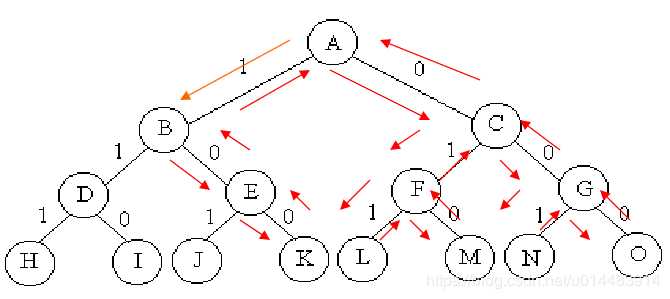
回溯法本质是用来搜索问题的解,典型地就是使用深度优先搜索,搜索路径一般沿树形结构进行,在搜索过程中,首先会判断所搜索的树结点是否包含问题的解,如果肯定不包含,则不再搜索以该结点为根的树结点,而向其祖先结点回溯;否则进入该子树,继续按深度优先策略搜索。
标签:while 0-1背包 turn cap 价值 inf 情况下 关于 树形结构
原文地址:https://www.cnblogs.com/hrnn/p/13346723.html