标签:min 广度优先遍历 wap nod 自己 minus 流程 load 贪心
广度优先遍历 Breadth-First-Search
这部分的内容也主要是学习了labuladong公众号内的相关讲解
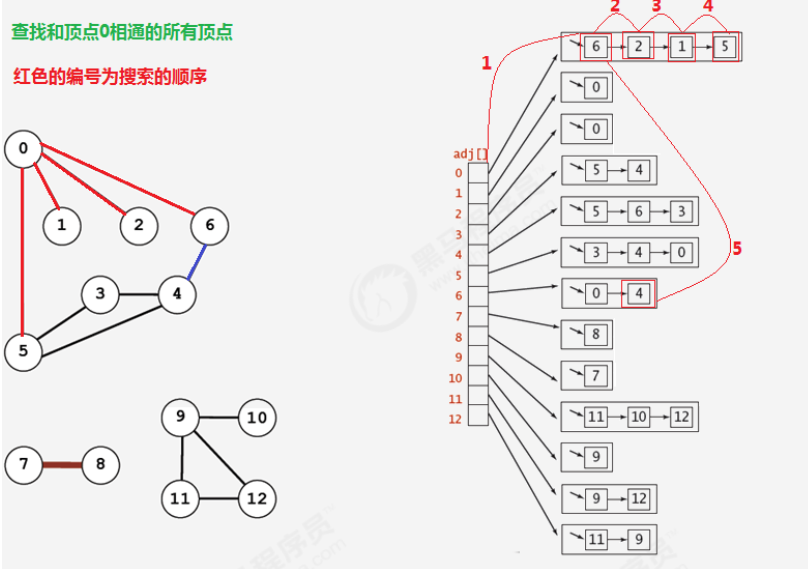
一般模版:
void bfs(Node start, Node target){
// 使用双端队列,而不是数组
Queue<TreeNode> queue = new ArrayDeque<>();
// 注意:ArrayDeque不允许null值,LinkedList允许null值
// Queue<TreeNode> queue = new LinkedList<>();
// 记录层数
int steps = 0;
// 记录访问过的节点
Set<Node> visited = new HashSet<>();
queue.offer(start);
while(!queue.isEmpty()){
// 当前层的节点数
int size = queue.size();
// 遍历当前层的所有节点数
for (int i=0; i<size; i++){
Node node = queue.poll();
result.add(node);
// 判断节点是否满足,而决定是否返回等操作
if(node.val == target.val){
return steps; // || return result;
}
// 将node周围的还未访问过的节点都加入队列中
for(Node tmp: node.adj()){
if(!visited.contains(tmp)){
queue.offer(tmp);
visited.add(tmp);
}
}
}
steps += 1; // 遍历完一层,层数+1
}
return;
}
相关题目:
针对树这种数据结构,因没有子节点回指向父节点的指针,因此可以不需要上述的 visited
void bfs(TreeNode root){
// 使用双端队列,而不是数组
Queue<TreeNode> queue = new ArrayDeque<>();
// 注意:ArrayDeque不允许null值,LinkedList允许null值
// Queue<TreeNode> queue = new LinkedList<>();
// 记录层数
int steps = 0;
queue.offer(root);
while(!queue.isEmpty()){
// 当前层的节点数
int size = queue.size();
// 遍历当前层的所有节点数
for (int i=0; i<size; i++){
TreeNode node = queue.poll();
result.add(node);
// 判断节点是否满足,而决定是否返回等操作
if(node.left != null){
queue.offer(node.left);
}
if(node.right != null){
queue.offer(node.right);
}
}
steps += 1; // 遍历完一层,层数+1
}
return;
}
典型题目:
513. 找树左下角的值,树专题已经做过了
在堆专题中涉及到了带权的最短距离,即此时的节点到邻居之间的距离不是定值了,而是带有权重。
使用优先队列的 BFS 实现典型的就是 dijkstra 算法。dijkstra 算法主要解决的是图中任意两点的最短距离。
算法的基本思想是贪心,每次都遍历所有邻居,并从中找到距离最小的,本质上是一种广度优先遍历。
更具体的内容跳转:堆专题-总结-四大应用-带权最短距离
深度优先遍历 Depth-First-Search,DFS,是一种用于遍历或搜索树或图的算法。
这里的 stack 可以理解为自己实现的栈,也可以理解为调用栈。如果是调用栈的时候就是递归,如果是自己实现的栈的话就是迭代。
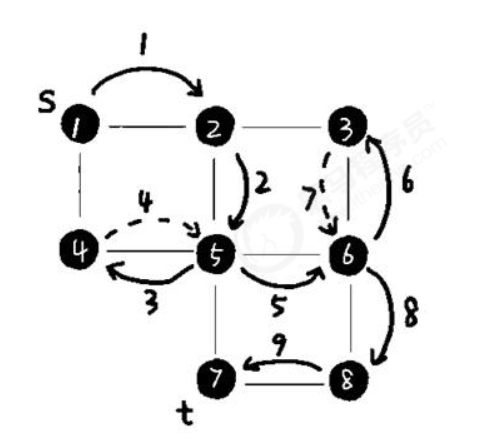
一个典型的通用的 DFS 模板可能是这样的:
boolean[] visited;
void dfs(int i) {
if (满足特定条件){
// 返回结果 or 退出搜索空间
}
visited[i] = true // 将当前状态标为已搜索
for (根据i能到达的下个状态j) {
if (!visited[j]) { // 如果状态j没有被搜索过
dfs(j)
}
}
}
public int openLock(String[] deadends, String target) {
// 记录需要跳过的死亡密码
Set<String> deads = new HashSet<>();
for(String s: deadends){
deads.add(s);
}
// 记录已经穷举过的密码,防止走回头路
Set<String> visited = new HashSet<>();
// 队列
Queue<String> queue = new LinkedList<>();
// 从起点开始进行BFS
int step = 0;
queue.offer("0000");
visited.add("0000");
while(!queue.isEmpty()){
// 当前层的节点数
int size = queue.size();
// 遍历当前层的所有节点数
for(int i=0; i<size; i++){
String cur = queue.poll();
// 判断节点是否相应条件
if(deads.contains(cur)) continue;
if(cur.equals(target)) return step;
// 周围的还未访问过的可能都加入队列中
for(int j=0; j<4; j++){
// 向上拨一个数字
String up = plusOne(cur, j);
if (!visited.contains(up)) {
queue.offer(up);
visited.add(up);
}
// 向下拨一个数字
String down = minusOne(cur, j);
if (!visited.contains(down)) {
queue.offer(down);
visited.add(down);
}
}
}
step += 1; // 遍历完一层,层数+1
}
// 如果穷举完都没找到目标密码,那就是找不到了
return -1;
}
// 将 s[j] 向上拨动一次
private String plusOne(String s, int j) {
char[] ch = s.toCharArray();
if (ch[j] == ‘9‘)
ch[j] = ‘0‘;
else
ch[j] += 1;
return new String(ch);
}
// 将 s[i] 向下拨动一次
private String minusOne(String s, int j) {
char[] ch = s.toCharArray();
if (ch[j] == ‘0‘)
ch[j] = ‘9‘;
else
ch[j] -= 1;
return new String(ch);
}
参考:BFS 算法框架套路详解
public int slidingPuzzle(int[][] board) {
/******* 准备工作 *******/
int m = 2, n = 3;
char[] start = new char[6];
char[] target = {‘1‘, ‘2‘, ‘3‘, ‘4‘, ‘5‘, ‘0‘};
// 将2*3转化为字符串
int index_s = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
start[index_s++] = (char)(board[i][j] + ‘0‘);
}
}
// 记录一维字符串的相邻索引
List<List<Integer>> neighbor = new ArrayList<>();
neighbor.add(Arrays.asList(1, 3));
neighbor.add(Arrays.asList(0, 2, 4));
neighbor.add(Arrays.asList(1, 5));
neighbor.add(Arrays.asList(0, 4));
neighbor.add(Arrays.asList(1, 3, 5));
neighbor.add(Arrays.asList(2, 4));
/******* BFS 算法框架开始 *******/
Queue<char[]> queue = new LinkedList<>();
Set<String> visited = new HashSet<>();
queue.offer(start);
visited.add(new String(start));
int steps = 0;
while(!queue.isEmpty()){
int size = queue.size();
for(int i=0; i<size; i++){
char[] cur = queue.poll();
// 判断是否达到目标局面
if(isEqual(cur, target)){
return steps;
}
// 找到数字 0 的索引
int index = 0;
for(; cur[index] != ‘0‘; index++);
// 将数字 0 和相邻的数字交换位置
for(Integer adj: neighbor.get(index)){
char[] tmp = new char[6];
System.arraycopy(cur, 0, tmp, 0, 6);
swap(tmp, index, adj);
if(!visited.contains(new String(tmp))){
queue.offer(tmp);
visited.add(new String(tmp));
}
}
}
steps++;
}
return -1;
}
private void swap(char[] chars, int i, int j){
char tmp = chars[i];
chars[i] = chars[j];
chars[j] = tmp;
}
private boolean isEqual(char[] a, char[] b){
if(a.length != b.length){
return false;
}
for(int i=0; i<a.length; i++){
if(a[i] != b[i]){
return false;
}
}
return true;
}
public int minDepth(TreeNode root) {
if(root == null){
return 0;
}
return bfs(root);
}
private int bfs(TreeNode root){
Queue<TreeNode> queue = new LinkedList<>();
// 记录层数
int steps = 1;
queue.offer(root);
while(!queue.isEmpty()){
// 当前层的节点数
int size = queue.size();
// 遍历当前层的所有节点数
for (int i=0; i<size; i++){
TreeNode node = queue.poll();
// 判断节点是否满足,而决定是否返回等操作
if(node.left == null && node.right == null){
return steps;
}
if(node.left != null){
queue.offer(node.left);
}
if(node.right != null){
queue.offer(node.right);
}
}
steps += 1;
}
return steps;
}
标签:min 广度优先遍历 wap nod 自己 minus 流程 load 贪心
原文地址:https://www.cnblogs.com/zhuchengchao/p/14401774.html