[LeetCode] 89. Gray Code

标签：pre   多个   new   enc   first   联系   接下来   seq   题意   

An n-bit gray code sequence is a sequence of 2n integers where:

• Every integer is in the inclusive range [0, 2n - 1],
• The first integer is 0,
• An integer appears no more than once in the sequence,
• The binary representation of every pair of adjacent integers differs by exactly one bit, and
• The binary representation of the first and last integers differs by exactly one bit.

Given an integer n, return any valid n-bit gray code sequence. 

Example 1:

Input: n = 2
Output: [0,1,3,2]
Explanation:
The binary representation of [0,1,3,2] is [00,01,11,10].
- 00 and 01 differ by one bit
- 01 and 11 differ by one bit
- 11 and 10 differ by one bit
- 10 and 00 differ by one bit
[0,2,3,1] is also a valid gray code sequence, whose binary representation is [00,10,11,01].
- 00 and 10 differ by one bit
- 10 and 11 differ by one bit
- 11 and 01 differ by one bit
- 01 and 00 differ by one bit

Example 2:

Input: n = 1
Output: [0,1]

Constraints:

• 1 <= n <= 16

格雷编码。

格雷编码是一个二进制数字系统，在该系统中，两个连续的数值仅有一个位数的差异。

给定一个代表编码总位数的非负整数 n，打印其格雷编码序列。即使有多个不同答案，你也只需要返回其中一种。

格雷编码序列必须以 0 开头。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/gray-code
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

这是一道二进制数字的题目，如果你知道格雷编码的公式那么会很简单，但是我这里给出一个动态规划的思路。这个思路可以在你不知道格雷编码公式的情况下也可以解决这道题。

题意中的格雷编码的定义是一个二进制数字系统，在该系统中，两个连续的数值仅有一个位数的差异。比如例子中给的

输入: 2
输出: [0,1,3,2]
解释:
00 - 0
01 - 1
11 - 3
10 - 2

对于给定的 n，其格雷编码序列并不唯一。
例如，[0,2,3,1] 也是一个有效的格雷编码序列。

00 - 0
10 - 2
11 - 3
01 - 1

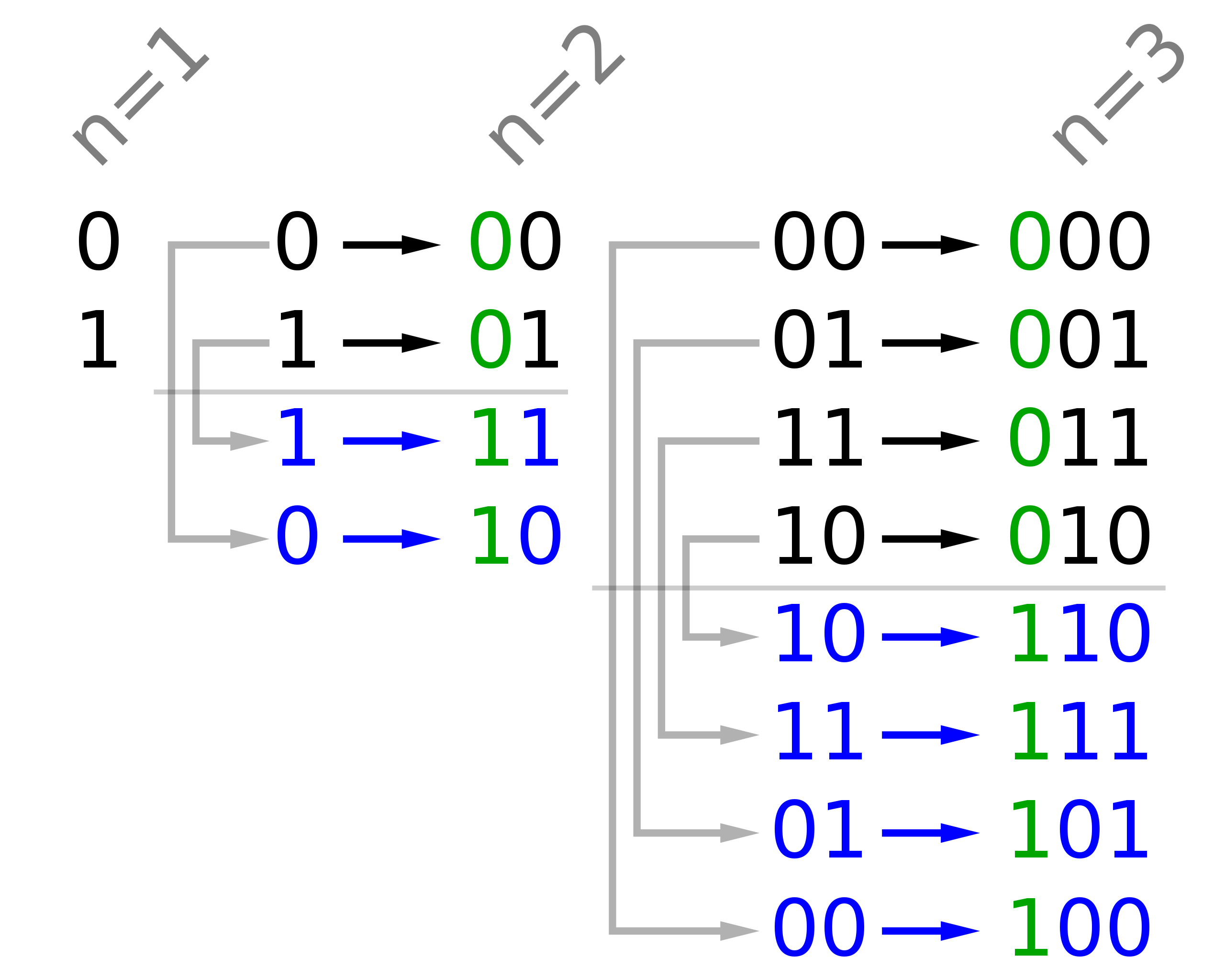
这里我给一个总结的很好的图示，数字 n - 1 的格雷编码可以作为数字 n 的格雷编码的一部分，同时数字 n - 1 的格雷编码的个数为 2^(n-1) 个，同时这前 2^(n-1) 个格雷编码是前一个数字的格雷编码每一个数字在最高位加一个 0，所以等同于没有加；接下来要找到数字 n 的格雷编码只需要再找到 2^(n-1) 个即可。这后半 2^(n-1) 个格雷编码，是把最高位加了一个 0 的那些数字全都改成 1，这样后半部分的数字和前半部分的数字依然只相差最高位那一位。

时间O(1)

空间O(n)

Java实现

 1 class Solution {
 2     private List<List<Integer>> dp;
 3 
 4     public List<Integer> grayCode(int n) {
 5         dp = new ArrayList<>(n + 1);
 6         for (int i = 0; i <= n; i++) {
 7             dp.add(new ArrayList<>(1 << i));
 8         }
 9         // 1. dp初始状态，即把数字0的格雷码先加入dp中
10         dp.get(0).add(0);
11         // 2. dp递推过程，通过循环依次计算数字1, 2, 3, ..., n 的格雷码
12         for (int num = 1; num <= n; num++) {
13             // 数字num的格雷码的总个数 2^num
14             int count = 1 << num;
15             for (int i = 0; i < count; i++) {
16                 int value;
17                 if (i < count / 2) {
18                     // 前半部分直接复制num - 1的格雷码
19                     value = dp.get(num - 1).get(i);
20                 } else {
21                     // 后半部分通过在首位添加1位1得到
22                     int add = 1 << (num - 1);
23                     value = dp.get(num).get(count - 1 - i) + add;
24                 }
25                 dp.get(num).add(value);
26             }
27         }
28         return dp.get(n);
29     }
30 }

LeetCode 题目总结

[LeetCode] 89. Gray Code

标签：pre   多个   new   enc   first   联系   接下来   seq   题意   

原文地址：https://www.cnblogs.com/cnoodle/p/14965295.html