标签:style http ar io os 使用 sp for on
在本节中,我们介绍Softmax回归模型,该模型是logistic回归模型在多分类问题上的推广,在多分类问题中,类标签  可以取两个以上的值。 Softmax回归模型对于诸如MNIST手写数字分类等问题是很有用的,该问题的目的是辨识10个不同的单个数字。Softmax回归是有监督的,不过后面也会介绍它与深度学习/无监督学习方法的结合。(译者注: MNIST 是一个手写数字识别库,由NYU 的Yann LeCun 等人维护。http://yann.lecun.com/exdb/mnist/ )
可以取两个以上的值。 Softmax回归模型对于诸如MNIST手写数字分类等问题是很有用的,该问题的目的是辨识10个不同的单个数字。Softmax回归是有监督的,不过后面也会介绍它与深度学习/无监督学习方法的结合。(译者注: MNIST 是一个手写数字识别库,由NYU 的Yann LeCun 等人维护。http://yann.lecun.com/exdb/mnist/ )
回想一下在 logistic 回归中,我们的训练集由 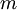 个已标记的样本构成:
个已标记的样本构成: ,其中输入特征
,其中输入特征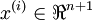 。(我们对符号的约定如下:特征向量
。(我们对符号的约定如下:特征向量  的维度为
的维度为 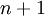 ,其中
,其中 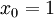 对应截距项 。) 由于 logistic 回归是针对二分类问题的,因此类标记
对应截距项 。) 由于 logistic 回归是针对二分类问题的,因此类标记 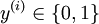 。假设函数(hypothesis function) 如下:
。假设函数(hypothesis function) 如下:
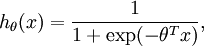
我们将训练模型参数  ,使其能够最小化代价函数 :
,使其能够最小化代价函数 :
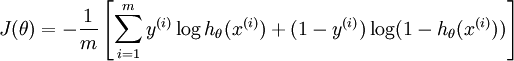
在 softmax回归中,我们解决的是多分类问题(相对于 logistic 回归解决的二分类问题),类标  可以取
可以取  个不同的值(而不是 2 个)。因此,对于训练集
个不同的值(而不是 2 个)。因此,对于训练集  ,我们有
,我们有 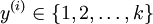 。(注意此处的类别下标从 1 开始,而不是 0)。例如,在 MNIST 数字识别任务中,我们有
。(注意此处的类别下标从 1 开始,而不是 0)。例如,在 MNIST 数字识别任务中,我们有 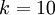 个不同的类别。
个不同的类别。
对于给定的测试输入  ,我们想用假设函数针对每一个类别j估算出概率值
,我们想用假设函数针对每一个类别j估算出概率值 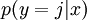 。也就是说,我们想估计
。也就是说,我们想估计  的每一种分类结果出现的概率。因此,我们的假设函数将要输出一个
的每一种分类结果出现的概率。因此,我们的假设函数将要输出一个  维的向量(向量元素的和为1)来表示这
维的向量(向量元素的和为1)来表示这  个估计的概率值。 具体地说,我们的假设函数
个估计的概率值。 具体地说,我们的假设函数 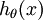 形式如下:
形式如下:
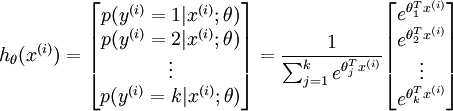
其中 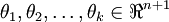 是模型的参数。请注意
是模型的参数。请注意 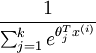 这一项对概率分布进行归一化,使得所有概率之和为 1 。
这一项对概率分布进行归一化,使得所有概率之和为 1 。
为了方便起见,我们同样使用符号  来表示全部的模型参数。在实现Softmax回归时,将
来表示全部的模型参数。在实现Softmax回归时,将  用一个
用一个 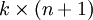 的矩阵来表示会很方便,该矩阵是将
的矩阵来表示会很方便,该矩阵是将 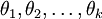 按行罗列起来得到的,如下所示:
按行罗列起来得到的,如下所示:
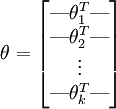
现在我们来介绍 softmax 回归算法的代价函数。在下面的公式中,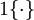 是示性函数,其取值规则为:
是示性函数,其取值规则为:
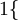
值为真的表达式
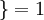
, 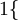 值为假的表达式
值为假的表达式 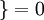 。举例来说,表达式
。举例来说,表达式 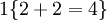 的值为1 ,
的值为1 ,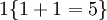 的值为 0。我们的代价函数为:
的值为 0。我们的代价函数为:
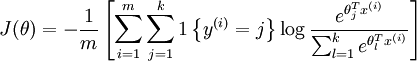
值得注意的是,上述公式是logistic回归代价函数的推广。logistic回归代价函数可以改为:
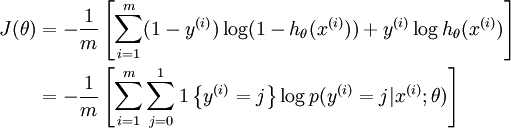
可以看到,Softmax代价函数与logistic 代价函数在形式上非常类似,只是在Softmax损失函数中对类标记的  个可能值进行了累加。注意在Softmax回归中将
个可能值进行了累加。注意在Softmax回归中将  分类为类别
分类为类别  的概率为:
的概率为:
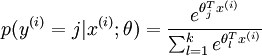 .
.
对于  的最小化问题,目前还没有闭式解法。因此,我们使用迭代的优化算法(例如梯度下降法,或 L-BFGS)。经过求导,我们得到梯度公式如下:
的最小化问题,目前还没有闭式解法。因此,我们使用迭代的优化算法(例如梯度下降法,或 L-BFGS)。经过求导,我们得到梯度公式如下:
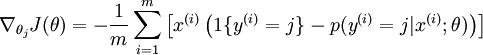
让我们来回顾一下符号 "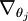 " 的含义。
" 的含义。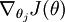 本身是一个向量,它的第
本身是一个向量,它的第  个元素
个元素 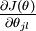 是
是  对
对 的第
的第  个分量的偏导数。
个分量的偏导数。
有了上面的偏导数公式以后,我们就可以将它代入到梯度下降法等算法中,来最小化  。 例如,在梯度下降法的标准实现中,每一次迭代需要进行如下更新:
。 例如,在梯度下降法的标准实现中,每一次迭代需要进行如下更新: 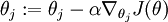 (
(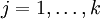 )。
)。
当实现 softmax 回归算法时, 我们通常会使用上述代价函数的一个改进版本。具体来说,就是和权重衰减(weight decay)一起使用。我们接下来介绍使用它的动机和细节。
Softmax 回归有一个不寻常的特点:它有一个“冗余”的参数集。为了便于阐述这一特点,假设我们从参数向量  中减去了向量
中减去了向量  ,这时,每一个
,这时,每一个  都变成了
都变成了 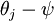 (
(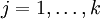 )。此时假设函数变成了以下的式子:
)。此时假设函数变成了以下的式子:
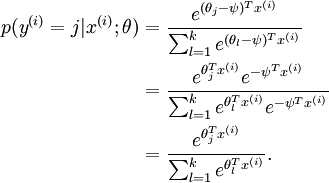
换句话说,从  中减去
中减去  完全不影响假设函数的预测结果!这表明前面的 softmax 回归模型中存在冗余的参数。更正式一点来说, Softmax 模型被过度参数化了。对于任意一个用于拟合数据的假设函数,可以求出多组参数值,这些参数得到的是完全相同的假设函数
完全不影响假设函数的预测结果!这表明前面的 softmax 回归模型中存在冗余的参数。更正式一点来说, Softmax 模型被过度参数化了。对于任意一个用于拟合数据的假设函数,可以求出多组参数值,这些参数得到的是完全相同的假设函数 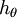 。
。
进一步而言,如果参数 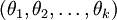 是代价函数
是代价函数  的极小值点,那么
的极小值点,那么 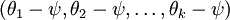 同样也是它的极小值点,其中
同样也是它的极小值点,其中  可以为任意向量。因此使
可以为任意向量。因此使  最小化的解不是唯一的。(有趣的是,由于
最小化的解不是唯一的。(有趣的是,由于  仍然是一个凸函数,因此梯度下降时不会遇到局部最优解的问题。但是 Hessian 矩阵是奇异的/不可逆的,这会直接导致采用牛顿法优化就遇到数值计算的问题)
仍然是一个凸函数,因此梯度下降时不会遇到局部最优解的问题。但是 Hessian 矩阵是奇异的/不可逆的,这会直接导致采用牛顿法优化就遇到数值计算的问题)
注意,当 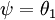 时,我们总是可以将
时,我们总是可以将  替换为
替换为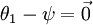 (即替换为全零向量),并且这种变换不会影响假设函数。因此我们可以去掉参数向量
(即替换为全零向量),并且这种变换不会影响假设函数。因此我们可以去掉参数向量  (或者其他
(或者其他  中的任意一个)而不影响假设函数的表达能力。实际上,与其优化全部的
中的任意一个)而不影响假设函数的表达能力。实际上,与其优化全部的 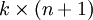 个参数
个参数 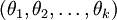 (其中
(其中 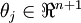 ),我们可以令
),我们可以令 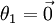 ,只优化剩余的
,只优化剩余的 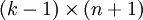 个参数,这样算法依然能够正常工作。
个参数,这样算法依然能够正常工作。
在实际应用中,为了使算法实现更简单清楚,往往保留所有参数 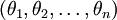 ,而不任意地将某一参数设置为 0。但此时我们需要对代价函数做一个改动:加入权重衰减。权重衰减可以解决 softmax 回归的参数冗余所带来的数值问题。
,而不任意地将某一参数设置为 0。但此时我们需要对代价函数做一个改动:加入权重衰减。权重衰减可以解决 softmax 回归的参数冗余所带来的数值问题。
我们通过添加一个权重衰减项 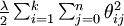 来修改代价函数,这个衰减项会惩罚过大的参数值,现在我们的代价函数变为:
来修改代价函数,这个衰减项会惩罚过大的参数值,现在我们的代价函数变为:
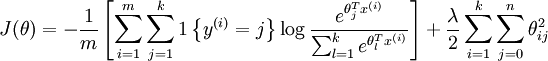
有了这个权重衰减项以后 (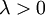 ),代价函数就变成了严格的凸函数,这样就可以保证得到唯一的解了。 此时的 Hessian矩阵变为可逆矩阵,并且因为
),代价函数就变成了严格的凸函数,这样就可以保证得到唯一的解了。 此时的 Hessian矩阵变为可逆矩阵,并且因为 是凸函数,梯度下降法和 L-BFGS 等算法可以保证收敛到全局最优解。
是凸函数,梯度下降法和 L-BFGS 等算法可以保证收敛到全局最优解。
为了使用优化算法,我们需要求得这个新函数  的导数,如下:
的导数,如下:
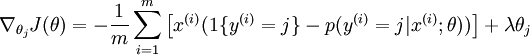
通过最小化  ,我们就能实现一个可用的 softmax 回归模型。
,我们就能实现一个可用的 softmax 回归模型。
当类别数 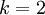 时,softmax 回归退化为 logistic 回归。这表明 softmax 回归是 logistic 回归的一般形式。具体地说,当
时,softmax 回归退化为 logistic 回归。这表明 softmax 回归是 logistic 回归的一般形式。具体地说,当 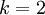 时,softmax 回归的假设函数为:
时,softmax 回归的假设函数为:
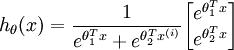
利用softmax回归参数冗余的特点,我们令 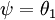 ,并且从两个参数向量中都减去向量
,并且从两个参数向量中都减去向量  ,得到:
,得到:
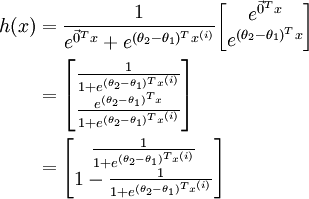
因此,用 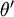 来表示
来表示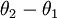 ,我们就会发现 softmax 回归器预测其中一个类别的概率为
,我们就会发现 softmax 回归器预测其中一个类别的概率为 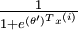 ,另一个类别概率的为
,另一个类别概率的为 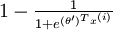 ,这与 logistic回归是一致的。
,这与 logistic回归是一致的。
如果你在开发一个音乐分类的应用,需要对k种类型的音乐进行识别,那么是选择使用 softmax 分类器呢,还是使用 logistic 回归算法建立 k 个独立的二元分类器呢?
这一选择取决于你的类别之间是否互斥,例如,如果你有四个类别的音乐,分别为:古典音乐、乡村音乐、摇滚乐和爵士乐,那么你可以假设每个训练样本只会被打上一个标签(即:一首歌只能属于这四种音乐类型的其中一种),此时你应该使用类别数 k = 4 的softmax回归。(如果在你的数据集中,有的歌曲不属于以上四类的其中任何一类,那么你可以添加一个“其他类”,并将类别数 k 设为5。)
如果你的四个类别如下:人声音乐、舞曲、影视原声、流行歌曲,那么这些类别之间并不是互斥的。例如:一首歌曲可以来源于影视原声,同时也包含人声 。这种情况下,使用4个二分类的 logistic 回归分类器更为合适。这样,对于每个新的音乐作品 ,我们的算法可以分别判断它是否属于各个类别。
现在我们来看一个计算视觉领域的例子,你的任务是将图像分到三个不同类别中。(i) 假设这三个类别分别是:室内场景、户外城区场景、户外荒野场景。你会使用sofmax回归还是 3个logistic 回归分类器呢? (ii) 现在假设这三个类别分别是室内场景、黑白图片、包含人物的图片,你又会选择 softmax 回归还是多个 logistic 回归分类器呢?
在第一个例子中,三个类别是互斥的,因此更适于选择softmax回归分类器 。而在第二个例子中,建立三个独立的 logistic回归分类器更加合适。
标签:style http ar io os 使用 sp for on
原文地址:http://www.cnblogs.com/alexanderkun/p/4171971.html