poj1463--hdu1054--Strategic Game（树形DP练习4）

标签：

Description

Bob enjoys playing computer games, especially strategic games, but sometimes he cannot find the solution fast enough and then he is very sad. Now he has the following problem. He must defend a medieval city, the roads of which form a tree. He has to put the minimum number of soldiers on the nodes so that they can observe all the edges. Can you help him? 

Your program should find the minimum number of soldiers that Bob has to put for a given tree. 

The input file contains several data sets in text format. Each data set represents a tree with the following description: 

the number of nodes 
the description of each node in the following format 
node_identifier:(number_of_roads) node_identifier1 node_identifier2 ... node_identifier 
or 
node_identifier:(0) 

The node identifiers are integer numbers between 0 and n-1, for n nodes (0 < n <= 1500). Every edge appears only once in the input data. 

For example for the tree: 



the solution is one soldier ( at the node 1). 

The output should be printed on the standard output. For each given input data set, print one integer number in a single line that gives the result (the minimum number of soldiers). An example is given in the following table: 

 

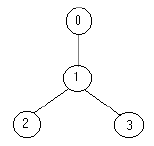
Sample Input

 4
0:(1) 1
1:(2) 2 3
2:(0)
3:(0)
5
3:(3) 1 4 2
1:(1) 0
2:(0)
0:(0)
4:(0)
        

 

Sample Output

 1
2 

 

给出有向图，要求找出用最少的人数可以看守所有的边。

dp[i][0] 以i为根的子树，i上不放人时，需要的最少人数。

dp[i][1] 以i为根的子树，i上放人时，需要的最少人数。

状态转移方程：j为i的子节点

dp[i][0] += dp[j][1] ;

dp[i][1] += max( dp[j][0],dp[j][1] ) ;

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std ;
struct node{
    int u , v ;
    int next ;
}edge[2000];
int head[2000] , cnt ;
int dp[2000][2] ;
void add(int u,int v)
{
    edge[cnt].u = u ; edge[cnt].v = v;
    edge[cnt].next = head[u] ;
    head[u] = cnt++ ;
    return ;
}
void dfs(int u)
{
    int i , v ;
    dp[u][0] = 0 ;
    dp[u][1] = 1 ;
    for(i = head[u] ; i != -1 ; i = edge[i].next)
    {
        v = edge[i].v ;
        dfs(v) ;
        dp[u][0] += dp[v][1] ;
        dp[u][1] += min(dp[v][0],dp[v][1]) ;
    }
    return ;
}
int main()
{
    int n , m , i , j , u , v , rt ;
    while( scanf("%d", &n) != EOF )
    {
        cnt = 0 ;
        rt = (n-1)*(n)/2 ;
        memset(head,-1,sizeof(head)) ;
        memset(dp,0,sizeof(dp)) ;
        for(i = 0 ; i < n ; i++)
        {
            scanf("%d:(%d)", &u, &m) ;
            while( m-- )
            {
                scanf("%d", &v) ;
                add(u,v) ;
                rt -= v ;
            }
        }
        dfs(rt) ;
        printf("%d\n", min(dp[rt][0],dp[rt][1])) ;
    }
    return 0;
}

poj1463--hdu1054--Strategic Game（树形DP练习4）

标签：

原文地址：http://blog.csdn.net/winddreams/article/details/42834113