poj1905--Expanding Rods(二分，精度伤不起啊)

标签：

Appoint description:  System Crawler  (2014-03-19)

Description

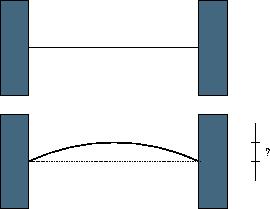When a thin rod of length L is heated n degrees, it expands to a new length L‘=(1+n*C)*L, where C is the coefficient of heat expansion. 
When a thin rod is mounted on two solid walls and then heated, it expands and takes the shape of a circular segment, the original rod being the chord of the segment. 

Your task is to compute the distance by which the center of the rod is displaced. 

Input

The input contains multiple lines. Each line of input contains three non-negative numbers: the initial lenth of the rod in millimeters, the temperature change in degrees and the coefficient of heat expansion of the material. Input data guarantee that no rod expands by more than one half of its original length. The last line of input contains three negative numbers and it should not be processed.

Output

For each line of input, output one line with the displacement of the center of the rod in millimeters with 3 digits of precision. 

Sample Input

1000 100 0.0001
15000 10 0.00006
10 0 0.001
-1 -1 -1

Sample Output

61.329
225.020
0.000

题意：题意很简单，计算膨胀后中点上升的高度（膨胀后变为一个圆弧）

二分上升的高度，最小为0，最大小于l/2 ， 枚举每一个x，带入公式中验证。

从三角形的公式中可以推出 r = l*l/(8*x) + x/2 ;

圆心角 = 2 * r * asin(l/(2.0*r)) ;

有了半径和圆心角就可以验证弧长对不对了。最终得到结果

注意：公式只能是这两个。。。。其他的公式（比如 sqrt(r*r - (l/2)*(l/2)) + x = r , 圆心角 = acos( 1 - l*l/(2*r*r) ) ）这些公式都会损失精度，至于为毛损失，天知道

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std ;
#define eqs 1e-8
double solve(double l,double x)
{
    double r , new_l ;
    r =  l*l/(8.0*x) + x/2.0 ;
    new_l = 2 * r * asin(l/(2.0*r)) ;
    return new_l ;
}
int main()
{
    double l , n , c , new_l , temp , last ;
    while( scanf("%lf %lf %lf", &l, &n, &c) != EOF )
    {
        if( l+n+c+3.0 < eqs ) break ;
        new_l = (1.0 + n*c) * l ;
        if( l == 0 || n == 0 || c == 0 )
        {
            printf("0.000\n") ;
            continue ;
        }
        double low , high , mid ;
        low = 0 ; high = l/2.0 ;
        while( high - low > eqs )
        {
            mid = ( high + low ) / 2.0 ;
            temp = solve(l,mid) ;
            if( new_l - temp >= eqs )
            {
                last = mid ;
                low = mid ;
            }
            else
                high = mid ;
        }
        printf("%.3lf\n", last) ;
    }
    return 0;
}

poj1905--Expanding Rods(二分，精度伤不起啊)

标签：

原文地址：http://blog.csdn.net/winddreams/article/details/43059633