标签:
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=5152 ,线段树区间更新 + 点更新 + 数论知识(数论是重点QAQ),好题值得一做。
BestCoder Round #24的C题,一道神题,不得不说,出题人的数论学的很好,很多人都没想到2333333不是素数的问题,当时全场爆零。我今天下午开始研究这道题,后来看了好久的标程才懂,惭愧。
一共有两个操作一个询问:1.询问[l , r]区间里的值的和; 2.将点x的值a[x]赋为2a[x]; 3.将区间[l , r]都加上x。
这道题复杂就是操作2了,这里需要先知道一个数论知识: 当x >= Phi(C)时, A^x = A ^ (x%Phi(C) + Phi(C)) (mod C). Phi(C)是C的欧拉函数,即1 ~ C中与C互素整数的个数,具体求法百度之。所以当操作2一直累积下去的时候应该是这样:
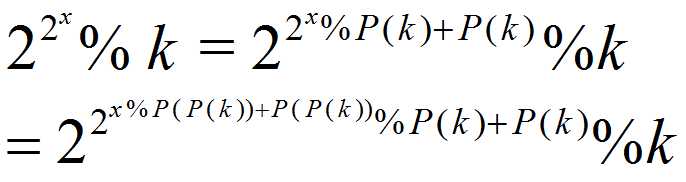
所以就是一直迭代求2333333的欧拉函数,对于2333333这个模数来说,求18次欧拉函数后就变成了1,所以保存到19层即可。接下来就是线段树的更新与求和。
具体解法:
这里只介绍操作2的部分:标程中用了一个一维的vector向量来保存两个信息:每个位置的操作2的次数和操作3要加的数,具体实现方法是vector <LL> a[N]后,如果i号位置需要进行操作2,则进行操作a[i].pushback(0),如果操作3的PushDown()更新到i的位置时,则a[i][a[i].size() - 1] += add[rt]; 表示在a[i][]数组的最后一个位置加上要加的数。这样的话a[i][]数组的长度就表示有多少次操作2,保存的值就代表了当时的操作3加上的值,所以每次迭代应该是num = 2num % phi[pos] + phi[pos] + a[...] (说点有点乱,不好意思~)。
还有一点要注意的是x < Phi(C)的情况,这样的话A ^ x 还等于 A ^ x,这样的话迭代就变为 num = 2num + a[...]. 这时候再判断num与当前层的欧拉函数的大小关系,到满足条件时再像公式中的进行即可。这里要注意一点,如果当前层满足 x >= Phi(C)的情况,则以后的每一层迭代结果必然也满足,因为 x % Phi(C) + Phi(C) 必然要大于Phi(C),这样传递下去就可以保证以后的都满足了...(- - ..还是说的很乱,具体见代码,虽然都是看的标程编的QAQ)。
#include <iostream>
#include <cstdio>
#include <vector>
#include <cmath>
#include <string>
#include <string.h>
#include <algorithm>
using namespace std;
#define LL __int64
#define eps 1e-8
#define INF INT_MAX
#define lson l , m , rt << 1
#define rson m + 1 , r , rt << 1 | 1
const int MOD = 2333333;
const int maxn = 50000 + 5;
int phi[20] = {2333333 , 2196720 , 580608 , 165888 , 55296 , 18432 , 6144 ,
2048 , 1024 , 512 , 256 , 128 , 64 , 32 , 16 , 8 , 4 , 2 , 1};
LL sum[maxn << 2] , add[maxn << 2];
vector <LL> a[maxn];
int pow2[33];
void init()
{ //求2 ^ i
for(int i = 0 ; i <= 30 ; i++)
pow2[i] = 1 << i;
}
LL pow_mod(LL a , LL i , LL n)
{ // a ^ i % n的快速幂
if(i == 0)
return 1;
LL tmp = pow_mod(a , i >> 1 , n);
tmp = tmp * tmp % n;
if(i & 1)
tmp = tmp * a % n;
return tmp;
}
void PushUp(int rt)
{
sum[rt] = (sum[rt << 1] + sum[rt << 1 | 1]) % MOD;
}
void build(int l , int r , int rt)
{
add[rt] = 0;
if(l == r) {
a[l].clear(); //清零不要忘了
scanf("%d" , &sum[rt]);
a[l].push_back(sum[rt]); //初始值放入a[l][0]
sum[rt] %= MOD;
return;
}
int m = (l + r) >> 1;
build(lson);
build(rson);
PushUp(rt);
}
void PushDown(int rt , int len)
{
if(add[rt]) {
add[rt << 1] += add[rt];
add[rt << 1 | 1] += add[rt];
sum[rt << 1] = (sum[rt << 1] + 1LL * (len - (len >> 1)) * add[rt]) % MOD;
sum[rt << 1 | 1] = (sum[rt << 1 | 1] + 1LL * (len >> 1) * add[rt]) % MOD;
add[rt] = 0;
}
}
void update(int L , int R , int x , int l , int r , int rt)
{
if(L <= l && R >= r) {
sum[rt] = (sum[rt] + 1LL * (r - l + 1) * x) % MOD;
add[rt] += x;
return;
}
PushDown(rt , r - l + 1);
int m = (l + r) >> 1;
if(L > m)
update(L , R , x , rson);
else if(R <= m)
update(L , R , x , lson);
else {
update(L , R , x , lson);
update(L , R , x , rson);
}
PushUp(rt);
}
int cal(vector <LL> a)
{
LL num;
if(a.size() < 19) { //没到18层,所以要全部来一遍
num = a[0];
bool flag = false; //flag判断是否满足 x >= Phi(C)
int pos = a.size() - 1;
if(num >= phi[pos]) {
flag = true;
num = num % phi[pos] + phi[pos];
}
pos--;
for(int i = 1 ; i < a.size(); i++ , pos--) {
if(flag) {
num = (pow_mod(2 , num , phi[pos]) + a[i]) % phi[pos] + phi[pos];
} else {
if(num >= 30) {
flag = true;
num = (pow_mod(2 , num , phi[pos]) + a[i]) % phi[pos] + phi[pos];
} else {
num = pow2[num] + a[i]; //这时就是 2 ^ num + a[i]
if(num >= phi[pos]) {
flag = true;
num = num % phi[pos] + phi[pos];
}
}
}
}
} else { //由于Phi[18]就等于1了,所以之前取余就都等于0,不管就可以了
num = 1;
int pos = 17;
for(int i = a.size() - 18 ; i < a.size() ; i++ , pos--) {
num = (pow_mod(2 , num , phi[pos]) + a[i]) % phi[pos] + phi[pos];
}
}
return num % MOD;
}
void modify(int p , int l , int r , int rt)
{
if(l == r) {
if(add[rt]) { //保留操作3的信息
a[p][a[p].size() - 1] += add[rt];
add[rt] = 0;
}
a[p].push_back(0); //加一层
sum[rt] = cal(a[p]);
return;
}
PushDown(rt , r - l + 1);
int m = (l + r) >> 1;
if(p <= m)
modify(p , lson);
else
modify(p , rson);
PushUp(rt);
}
int query(int L , int R , int l , int r , int rt)
{
if(L <= l && R >= r) {
return sum[rt] % MOD;
}
PushDown(rt , r - l + 1);
int m = (l + r) >> 1;
if(L > m)
return query(L , R , rson);
else if(R <= m)
return query(L , R , lson);
else
return (query(L , R , lson) + query(L , R , rson)) % MOD;
}
int main()
{
init();
int a , b , c , n , m , ch;
while(~scanf("%d %d" , &n , &m))
{
build(1 , n , 1);
while(m--) {
scanf("%d" , &ch);
if(ch == 1) {
scanf("%d %d" , &a , &b);
printf("%d\n" , query(a , b , 1 , n , 1));
} else if(ch == 2) {
scanf("%d" , &c);
modify(c , 1 , n , 1);
} else {
scanf("%d %d %d" , &a , &b , &c);
update(a , b , c , 1 , n , 1);
}
}
}
return 0;
}
另附欧拉函数的代码:
int Euler(int n)
{
vector <int> a;
int i = 2;
int res = n;
while(n != 1) {
if(n % i == 0)
a.push_back(i);
while(n % i == 0)
n /= i;
i++;
}
for(i = 0 ; i < a.size() ; i++)
res = res / a[i] * (a[i] - 1);
return res;
}
标签:
原文地址:http://www.cnblogs.com/H-Vking/p/4312177.html