标签:
神经元的简单模型
Idealized neurons
• To model things we have to idealize them (e.g. atoms)
– Idealization removes complicated details that are not essential for understanding the main principles.
– It allows us to apply mathematics and to make analogies to other, familiar systems.
– Once we understand the basic principles, its easy to add complexity to make the model more faithful.
• It is often worth understanding models that are known to be wrong (but we must not forget that they are wrong!)
– E.g. neurons that communicate real values rather than discrete spikes of activity.
Linear neurons
• These are simple but computationally limited
– If we can make them learn we may get insight into more complicated neurons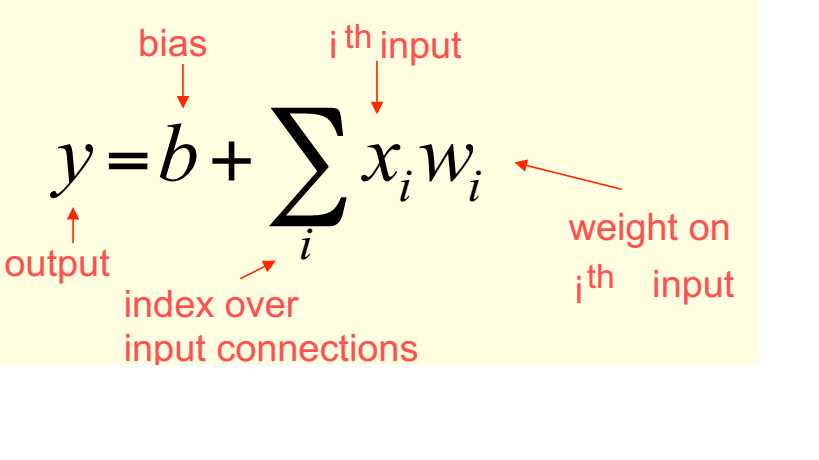
Binary threshold neurons 二值阈值神经元
McCulloch-Pitts (1943): influenced Von Neumann.
– First compute a weighted sum of the inputs.
– Then send out a fixed size spike of activity if the weighted sum exceeds a threshold.
– McCulloch and Pitts thought that each spike is like the truth value of a proposition and compute the truth value of another proposition!
There are two equivalent ways to write the equations for a binary threshold neuron:
Rectified Linear Neurons
(sometimes called linear threshold neurons)
They compute a linear weighted sum of their inputs.
The output is a non-linear function of the total input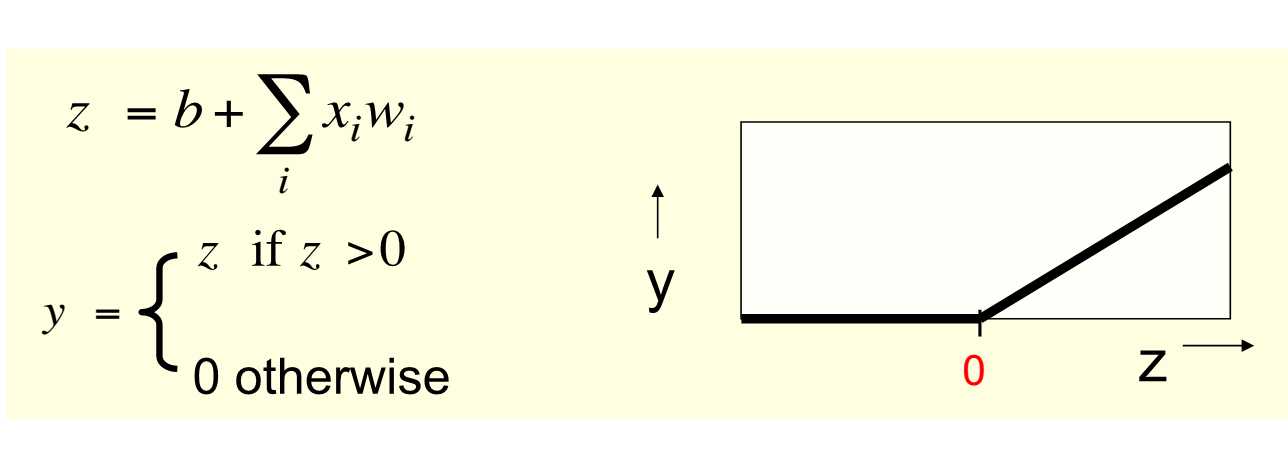
Sigmoid neurons 这个神经元经常使用
These give a real-valued output that is a smooth and bounded function of their total input.
– Typically they use the logistic function
– They have nice smooth derivatives, the derivatives change continuously and they‘re nicely behaved and they make it easy to do learning.
Stochastic binary neurons 随机二进制神经元
These use the same equations as logistic units.
– But they treat the output of the logistic as the probability of producing a spike in a short time window.
Instead of outputtiing that probability as a real number they actually make a probabilistic decision, and so what they acutally output is either a one or a zero. They‘re intrisically random. So they‘re treating the P as the probability of producing a one, not as a real number.
• We can do a similar trick for rectified(改正的) linear units:
– The output is treated as the Poisson rate for spikes.
So the rectified linear unit determines the rate, but intrinsic randomness in the unit determines when the spikes are actually produced.
标签:
原文地址:http://www.cnblogs.com/jinee/p/4472585.html