标签:
最近要研究四轴飞行器的控制相关的问题,网上详尽的讲述四轴建模的文章好像不多,在这里总结一下。
我们看网上的好多关于四轴飞行器的文章,尤其是讲他的控制的文章,大都要用一个章节讲一下四轴的动态模型。那么为什么要建立模型?当然四轴是个欠驱动系统,控制4个轴却要提供他的6个自由度(上下左右前后运动和三个方向角,如果是六轴就不再是欠驱动的),所以建模是必要的。这是我们看到的很多文档的陈述。在这里我想说一下我的理解,之所以研究控制需要知道他的模型,是因为我们要控制这个飞行器,就需要知道给他一个输入,他会对应一个怎样的输出,这样的对应关系就是一个模型。例如我们采用PID的反馈控制系统,采用角度环作为参考量,那么我们就需要知道,我给你四轴一个特定的控制,你此刻要对应一个怎样的角度给我,如果给我的和模型不相符,那么这个不相符就是误差,消除误差我们才能控制的“好”。如果我们没有模型那就不知道对应关系也就不知道什么叫控制的“好”了。再举一个例子,假设我们给坦克一个100的油门,他的速度是50,给汽车一个100的油门,他对应的速度是100(有点牵强,就是个比喻,假设给了坦克和汽车一样的控制量),这里坦克对应50 和汽车对应100的速度就是根据他们的模型推断出来的。我们也正是知道了他们的模型,才会知道给定输入,这家伙会输出多少。这就是建模的意义。
四轴虽然组装和调试相对简单(多说一句,我曾经认为直升机比四轴简单,后来看了一下直升机的机械结构,果断转变了看法),但是解决其建模问题还是比较复杂的。在这里我想复习一下基础知识,告别力学多年,在看这些方程的时候也是云里雾里。
角速度和角加速度的大小方向,与转矩线速度的关系一直理解的不透彻。总结一下希望能够明白点。

图中讲的是在一个旋转系统里,作用力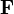 、位置矢量
、位置矢量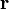 、力矩
、力矩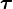 、动量
、动量 、角动量
、角动量 ,这些物理量之间的关系。
,这些物理量之间的关系。
(1)角速度
角速度刻画角位移随时间的变化率,一般用ω表示。二维情况下:初中物理上讲,一定点绕定点转动,则旋转半径上各点的角速度是一样的,不同的是线速度,且有 v=ωr,r代表所求点的旋转半径。
三维情况下: v=ω×r,其中,×表示矢量相乘(叉乘),方向由右手螺旋定则确定,r旋转半径,方向由圆心向外。
(2)角加速度
一般用a表示加速度,或者用我们经常在文献中看见的角度的二次导,角速度的一次导。
百度百科角加速度的方向给出了推导定义,上面定义角速度的时候,我们有 v=ω×r,则两边同时求导数,我们有:a = α × OP(其中a,α,OP均为矢量,此处为向量积),由此公式可得角加速度的方向和大小。
写成标量形式有:|a| = |α| |OP| sinθ,即:|a| = |α| r
如果运动固定为圆周运动,r是一个常数,那么角加速度大小等于|a|/r ,方向跟ω方向相同。
(3)转矩、扭矩
(4)转动惯量(Moment of Inertial)
(5)动量(Momentum)
给出公式:p=mv,质量组的动量为组内各质点动量的矢量和。
(6)角动量(angular momentum)
角动量刻画了物体到原点的位移和动量相关的物理量,一般用L 表示。

标签:
原文地址:http://blog.csdn.net/junshen1314/article/details/45643819