标签：

动态规划dynamic programming

June,7, 2015

作者：swanGooseMan

出处：http://www.cnblogs.com/swanGooseMan/p/4556588.html

1. 什么是动态规划？

• dynamic programming is a method for solving a complex problem by breaking it down into a collection of simpler subproblems.（引自维基百科）
• 动态规划是通过拆分问题，定义问题状态和状态之间的关系，使得问题能够以递推（或者说分治）的方式去解决。
• 如何拆分问题，是动态规划的核心。而拆分问题，靠的就是状态和状态转移方程的定义。
• 动态规划的本质（两个重要的概念）：状态（形如dp[i][j]）、状态转移方程（形如dp[i][j] = dp[i - 1][j] + dp[i -1][j – 1]）

动态规划相关的其他几个名词：

a. “缓存”，“重叠子问题”，“记忆化”：
这三个名词，都是在阐述递推式求解的技巧。以Fibonacci数列为例，计算第100项的时候，需要计算第99项和98项；在计算第101项的时候，需要第100项和第99项，这时候你还需要重新计算第99项吗？不需要，你只需要在第一次计算的时候把它记下来就可以了。
上述的需要再次计算的“第99项”，就叫“重叠子问题”。如果没有计算过，就按照递推式计算，如果计算过，直接使用，就像“缓存”一样，这种方法，叫做“记忆化”，这是递推式求解的技巧。这种技巧，通俗的说叫“花费空间来节省时间”。都不是动态规划的本质，不是动态规划的核心。

b. "无后效性"，“最优子结构”：
上述的状态转移方程中，等式右边不会用到下标大于左边i或者j的值，这是"无后效性"的通俗上的数学定义，符合这种定义的状态定义，我们可以说它具有“最优子结构”的性质，在动态规划中我们要做的，就是找到这种“最优子结构”。

c. “递归”：
递归是递推式求解的方法。

2. 怎么用动态规划？

• 通常用来求解最优化问题(optimization problem): 这类问题可以有很多可行的解，我们需要找出其中的最优解。应用于子问题重叠的情况。
• 动态规划通过拆分问题，对每个子问题只求解一次，将其解保存在一个表格（数组）中，从而无需每次求解一个子子问题时都重新计算，当前子问题的解将由上一次子问题的解推出，只需要多项式时间复杂度，因此它比回溯法、暴力法等要快许多。

通常按如下四个步骤来设计动态规划算法：

1. 刻画一个最优解的结构特征

2. 递归地定义最优解的值

3. 计算最优解的值，通常采用自底向上（如Fibonacci从1开始）的方法。也可以自顶向下（如Fibonacci从n开始）进行求解，但此时需要对解需要进行记录。//此3步构成动态规划解的基础。

4. 利用计算出的最优解的信息构造一个最优解。//此步如果只要求计算最优解的值时，可省略。

即对于具有最优子结构、重叠子问题的最优化问题，通过拆分问题，找出满足无后效性的状态和状态转移方程。（这也是DP的难点所在）

3. 实例

DP1：1447 采药

问题描述：

辰辰是个天资聪颖的孩子，他的梦想是成为世界上最伟大的医师。为此，他想拜附近最有威望的医师为师。医师为了判断他的资质，给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说：“孩子，这个山洞里有一些不同的草药，采每一株都需要一些时间，每一株也有它自身的价值。我会给你一段时间，在这段时间里，你可以采到一些草药。如果你是一个聪明的孩子，你应该可以让采到的草药的总价值最大。” 如果你是辰辰，你能完成这个任务吗？

分析：

将问题分解成若干子问题，让问题规模变小

对于最终最优结果(达到最大价值)，假如第N个药品没有采，那么最优结果就是总时间为totalTim内采n-1个物品的最大价值。

对于n-1如果不是最大价值（即有比它更大的），那么与最优结果的假设（第N个药品没有采）矛盾，所以满足最优子结构性质，可以使用动态规划算法。

拆分问题：

在totalTime（70）时间内采摘totalDrug（3）药草，最终达到最大价值，根据第N（3）个物品是否采摘，可分为两种情况：

子问题1：第N个物品没有采摘。即在totalTime（70）时间内继续采摘totalDrug-1（2）药草。

子问题2：第N个物品有采摘。即在totalTime – time（n）（69）时间内继续采摘totalDrug-1（2）药草，此时最优价值应加上该物品的价值vlan（n）（2）。

状态： time时间内采摘drug颗药草的最大价值dp[drug][time]

状态转移方程：dp[drug][time] = max { dp[drug-1][time] , dp[drug-1][time - time(n)]+vlan(n) }，即dp[n][m] = 较大值{dp[n-1][m], dp[n-1][m-time[n]]+value[n] }

AC源码：

#include <iostream>
#include <cstdio>
using namespace std;

//物品数组，结构体，时间，价值
typedef struct {
    int time;
    int value;
}Drug;
Drug drug[101];

int main() {
    int totalTime, totalDrug;//总采药时间，总药品数

    int dp[101][1001]={0};//记录表格  dp[总药品数][总采药时间]

    //读入数据
    // freopen("input.txt", "r", stdin);
    scanf("%d%d", &totalTime, &totalDrug);
    for (int i = 1; i <= totalDrug; i++) {
        scanf("%d%d", &drug[i].time, &drug[i].value);
    }

    //DP
    for (int i = 1; i <= totalDrug; i++) {
        for (int j = 1; j <= totalTime; j++) {  //取两个子问题的最大值
            dp[i][j] = dp[i-1][j];  //子问题1: 第N个物品没有采摘
            if (drug[i].time <= j && dp[i][j] < dp[i-1][j-drug[i].time] + drug[i].value) {  //子问题2: 第N个物品有采摘
                dp[i][j] = dp[i-1][j-drug[i].time] + drug[i].value;
            }
        }
    }
    printf("%d\n", dp[totalDrug][totalTime]);
    return 0;
}

View Code

DP2 ：1448最长上升子序列(Longest Increasing Subsequence)

问题描述：

一个数的序列bi，当b1 < b2 < ... < bS的时候，我们称这个序列是上升的。对于给定的一个序列(a1, a2, ..., aN)，我们可以得到一些上升的子序列(ai1, ai2, ..., aiK)，这里1 <= i1 < i2 < ... < iK <= N。比如，对于序列(1, 7, 3, 5, 9, 4, 8)，有它的一些上升子序列，如(1, 7), (3, 4, 8)等等。这些子序列中最长的长度是4，比如子序列(1, 3, 5, 8).

你的任务，就是对于给定的序列，求出最长上升子序列的长度。

拆分问题：

原问题含n项序列的LIS长度，等价于以第1,2,3,...,n项结尾的LIS长度集合中的最大值，由此拆分为n个子问题，最后求出n个LCS的最大者：

n个子问题：以第n项结尾的LIS的长度是：保证第i项比第n项小的情况下，以第i项结尾的LIS长度加一的最大值，取遍i的所有值（i小于n）。

即max{dp[i]+1},其中 1<=i<=n-1 且 array[i] < array[n]

状态：数列中以第n项结尾的最长上升子序列的长度 dp[n]

状态转移方程：

dp[1] = 1;（根据状态定义导出边界情况）

dp[n] = max{dp[i]+1}，其中 1<=i<=n-1 且 array[i] < array[n]

AC源码：

#include <iostream>
#include <cstdio>
using namespace std;

int lcs(int array[],int n) {
  int dp[n];
  int max = 1;  //整个序列的最长递增子序列长度,至少为1
  for (int i = 0; i < n; ++i) {  //遍历整个序列,分别求出n个子问题的解dp[i]
    dp[i] = 1;  //以第i项结尾的LIS长度,至少为1,下面进行计算
  //dp[i]:保证第i项比第n项小的情况下，以第i项结尾的LIS长度加一的最大值.
    for (int j = 0; j < i; ++j) {  //遍历前0 ~ i-1 项
      if(array[j] < array[i] && dp[i] < dp[j] + 1)
        dp[i] = dp[j] + 1;
    }
    if(max < dp[i]) max =dp[i];
  }
  return max;
}

int main(int argc, char const *argv[]) {
// #ifndef _OJ_  //ONLINE_JUDGE
  // freopen("input.txt", "r", stdin);
//   freopen("output.txt","w",stdout);
// #endif
  int n;
  int array[1001];
  scanf("%d", &n);
  for (int i = 0; i < n; ++i)
    scanf("%d", &array[i]);
  printf("%d\n", lcs(array, n));
  return 0;
}

View Code

DP4：1450 最长公共子序列（Longest Common Subsequence）

问题描述：

需要你做的就是写一个程序，得出最长公共子序列。
最长公共子序列也称作最长公共子串(不要求连续)，英文缩写为LCS（Longest Common Subsequence）。其定义是，一个序列S ，如果分别是两个或多个已知序列的子序列，且是所有符合此条件序列中最长的，则S 称为已知序列的最长公共子序列。

问题拆分：

最长公共子序列的结构有如下表示：

设序列X=<x1, x2, …, xm>和Y=<y1, y2, …, yn>的一个最长公共子序列Z=<z1, z2, …, zk>，则可分为以下三种情况：

1. 若xm=yn，则zk=xm=yn且Zk-1是Xm-1和Yn-1的最长公共子序列；

2. 若xm≠yn且zk≠xm ，则Z是Xm-1和Y的最长公共子序列；

3. 若xm≠yn且zk≠yn，则Z是X和Yn-1的最长公共子序列。

其中Xm-1=<x1, x2, …, xm-1>，Yn-1=<y1, y2, …, yn-1>，Zk-1=<z1, z2, …, zk-1>。

状态：

用dp[i,j]记录序列Xi和Yj的最长公共子序列的长度。其中Xi=<x1, x2, …, xi>，Yj=<y1, y2, …, yj>。

状态转移方程：

当i=0或j=0时，空序列是Xi和Yj的最长公共子序列，故dp[i,j]=0。其他情况下，由定理可建立递归关系如下：

　　　　| 0 　　　　　　　　 　　　　if i=0 or j=0

dp[i][j] = | dp[i-1][j-1] 　　　　　　　　 if i>0 , j>0 and Xi == Yj

　　　　| max{dp[i][j-1], dp[i-1][j]} 　　 if i>0 , j>0 and Xi != Yj

 AC源码：

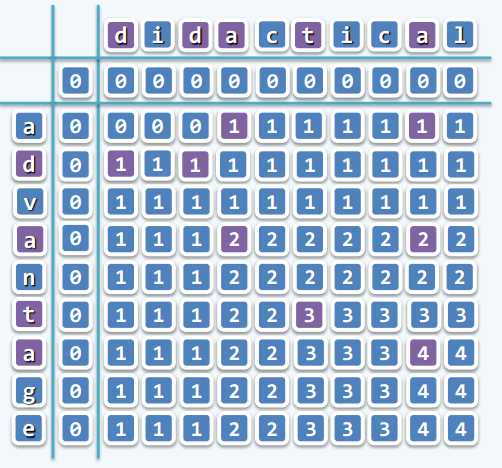
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
using namespace std;

int lcs(char s1[], char s2[]) {
  int maxlen = 0;
  int len1 = strlen(s1), len2 = strlen(s2);
  int dp[len1 + 1][len2 + 1];  //状态: dp[i,j]记录序列 Xi 和 Yj 的最长公共子序列的长度
  for (int i = 0; i < len1 + 1; ++i) dp[i][0] = 0;  //根据状态定义导出边界情况 (任一序列与空序列的lcs为0)
  for (int i = 0; i < len2 + 1; ++i) dp[0][i] = 0;
  for (int i = 1; i < len1 + 1; ++i) {  //算法核心, 根据状态转移方程, 自底向上计算.
    for (int j = 1; j < len2 + 1; ++j) {
      if (s1[i - 1] == s2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
      else dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
      maxlen = max(maxlen,dp[i][j]);
    }
  }
  return maxlen;
}

int main(int argc, char const *argv[]) {
// #ifndef _OJ_  //ONLINE_JUDGE
  // freopen("input.txt", "r", stdin);
//   // freopen("output.txt", "w", stdout);
// #endif
  int n;
  char s1[1010], s2[1010];
  scanf("%d", &n);
  while (n--) {
    scanf("%s%s", s1, s2);
    // gets(s1); gets(s2);
    printf("%d\n", lcs(s1,s2));
  }
  return 0;
}

View Code

动态规划 dynamic programming

标签：

原文地址：http://www.cnblogs.com/swanGooseMan/p/4556588.html