摘录-Introduction to Statistical Learning Theory(统计机器学习导论)

标签：learning   size   不等式   最小   span   png   分析   learn   nbsp   

机器学习目标：（二分类）

经验风险：

过度拟合：

经验风险最小化：

结构风险最小化：

正则：

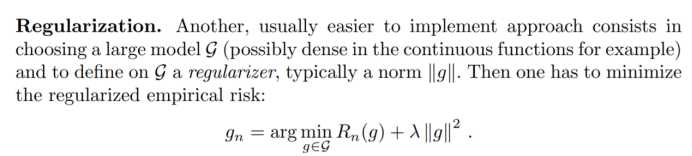
特点：

误差错误估计错误：

误差上界分析：

R(g)的经验风险上界：

对错误分类的误差F定义(值域[0或1])：

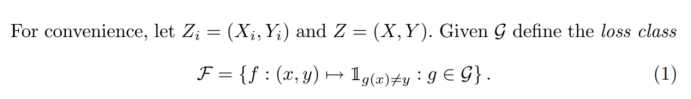
F和R的关系：

关于F的Hoe不等式：

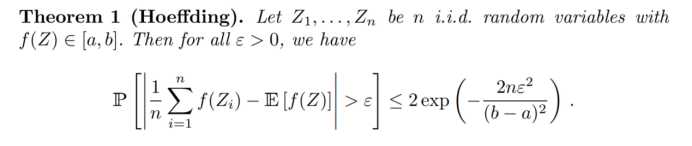
意义：

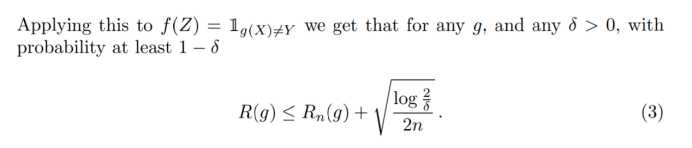
统一上界：

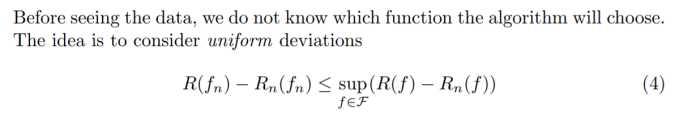
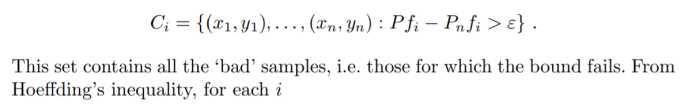
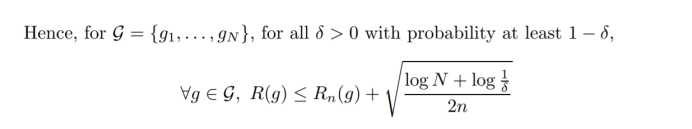
与Hoe的差异：

增长函数：

VC维：

VC维无限的函数族：

证明：将给定的点进行+-+-划分，如果有连续++或--的点在中间添加一个新点，保证一正一负，寻求一个sin函数的零点刚好过以上所有点时，给定一个微小增量t’，sin((t’)x)可满足条件。寻找方法是求出所有相邻点的距离，进行分子有理化，提公分母，求出所有分子最大公约数，乘以公分母即为所有点的一个单位长度，也是sin函数的半周期，可求出t。

典型的生长函数：

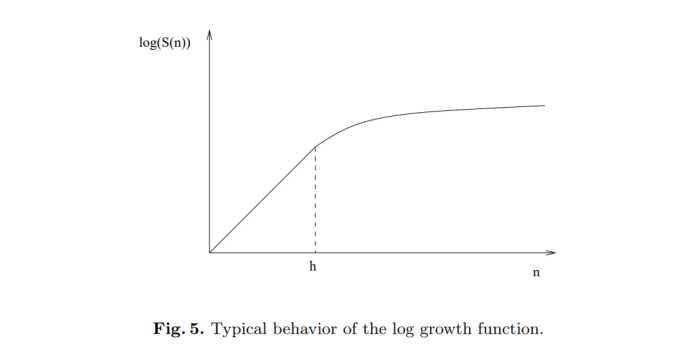
VC维与R(g)的关系：

VC商（分布相关）：

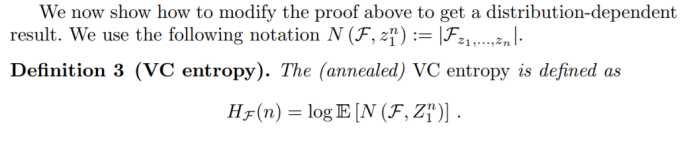
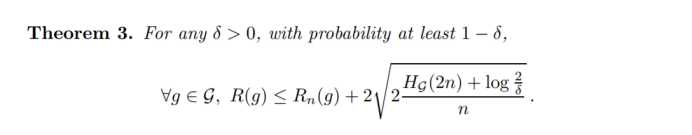
Covering Numbers：与VC维，VC商，生长函数一样描述函数特特性

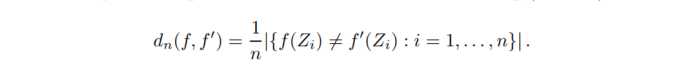
Rademacher averages：

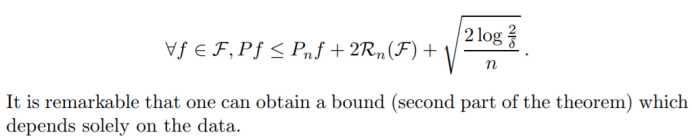
（意义在于仅仅依靠样本就能确定出边界）

摘录-Introduction to Statistical Learning Theory(统计机器学习导论)

标签：learning   size   不等式   最小   span   png   分析   learn   nbsp   

原文地址：http://www.cnblogs.com/jkserge/p/7091476.html