CNN详解

标签：函数   cti   深度学习   解决   数据处理   tar   ann   不为   out   

CNN详解

版权声明：本文为博主原创文章，转载请指明转载地址

http://www.cnblogs.com/fydeblog/p/7450413.html

前言

这篇博客主要就是卷积神经网络（CNN）的历史、模块、特点和架构等等

1. CNN历史

• CNN最早可以追溯到1968Hubel和Wiesel的论文，这篇论文讲述猫和猴的视觉皮层含有对视野的小区域单独反应的神经元，如果眼睛没有移动，则视觉刺激影响单个神经元的视觉空间区域被称为其感受野（Receptive Field）。相邻细胞具有相似和重叠的感受野。感受野大小和位置在皮层之间系统地变化，形成完整的视觉空间图。这个为CNN的局部感知奠定了一个基础。
• 然后是1980年，神经感知机(neocognitron)的提出，标志了第一个初始的卷积神经网络的诞生，也是感受野概念在人工神经网络领域的首次应用，神经认知机将一个视觉模式分解成许多子模式（特征），然后进入分层递阶式相连的特征平面进行处理。
• 在然后1988年，时不变神经网络(Shift-invariant neural network)的提出，将卷积神经网络的功能进行了一次提高，使其能够在即使物体有位移或轻微变形的时候，也能完成识别。
• 卷积神经网络的前馈架构在神经抽象金字塔（Neural abstraction pyramid）中被横向和反馈连接扩展。所产生的复现卷积网络允许灵活地并入情景信息以迭代地解决局部模糊。与以前的模型相反，产生了最高分辨率的图像输出。
• 最后，2005出现了一篇GPU实现CNN的paper，标志了一种实现CNN更有效的方式，之后在2012年ImageNet大赛中CNN由于其高精确度脱颖而出，于是，深度学习正式进入人们的视野。

2 CNN基本模块

CNN由输入和输出层以及多个隐藏层组成，隐藏层可分为卷积层，池化层、RELU层和全连通层。

2.1 输入层

CNN的输入一般是二维向量，可以有高度，比如，RGB图像

2.2 卷积层

卷积层是CNN的核心，层的参数由一组可学习的滤波器（filter）或内核（kernels）组成，它们具有小的感受野，延伸到输入容积的整个深度。 在前馈期间，每个滤波器对输入进行卷积，计算滤波器和输入之间的点积，并产生该滤波器的二维激活图（输入一般二维向量，但可能有高度（即RGB））。 简单来说，卷积层是用来对输入层进行卷积，提取更高层次的特征。

联想理解：

• 可能上面的话语太拗口，这里讲一下卷积的作用，我最早接触卷积是在信号与系统这门课上。在信号与系统中，输入对一个系统的响应是等于输入信号e(x)与系统函数h(x)进行卷积，h(x)可以看作一个滤波器，它会对输入信号进行筛选，选择和它类似的信号，其他则过滤掉，相信学过的人有这个体会哈！
• 我们还可以想想数字图像处理（DIP）这门课，我们在提取图像的边缘特征时，用到的一个卷积核，名字叫sobel算子，它与图像进行卷积，就可以得到边缘，这个原因是有sobel算子与图像边缘的结构相似，所以才能提取出来，这个可能更容易理解卷积层的作用吧，但不同的是这里的卷积层参数未知，需要学习才能得到。

2.3 池化层

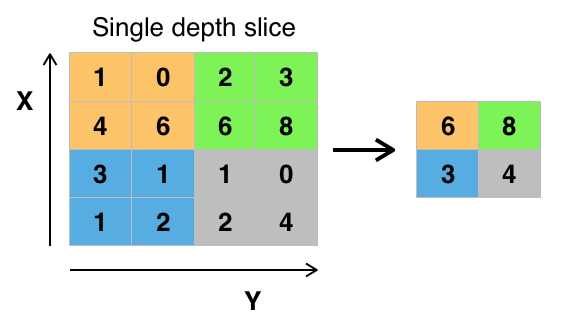
池化层又称下采样，它的作用是减小数据处理量同时保留有用信息，它是怎么做到的呢？

答：通常池化层是每邻域四个像素中的最大值变为一个像素（这就是下一讲要降的max_pooling），为什么可以这么做呢？这是因为卷积已经提取出特征，相邻区域的特征是类似，近乎不变，这是池化只是选出最能表征特征的像素，缩减了数据量，同时保留了特征，何乐而不为呢？池化层的作用可以描述为模糊图像，丢掉了一些不是那么重要的特征.

图形描述：

2.4 RELU层

这个RELU我们之前讲过，全名将修正线性单元，是神经元的激活函数，对输入值x的作用是max(0,x)，当然RELU只是一种选择，还有选sigmiod等等

2.5 全连通层

这个层就是一个常规的神经网络，它的作用是对经过多次卷积层和多次池化层所得出来的高级特征进行全连接（全连接就是常规神经网络的性质），算出最后的预测值。

2.6 输出层

输出层就不用介绍了，就是对结果的预测值，一般会加一个softmax层。

3. CNN的特点

这里主要讨论CNN相比与传统的神经网络的不同之处，CNN主要有三大特色，分别是局部感知、权重共享和多卷积核

3.1 局部感知

局部感知就是我们上面说的感受野，实际上就是卷积核和图像卷积的时候，每次卷积核所覆盖的像素只是一小部分，是局部特征，所以说是局部感知。CNN是一个从局部到整体的过程（局部到整体的实现是在全连通层），而传统的神经网络是整体的过程。

图形描述：

3.2 权重共享

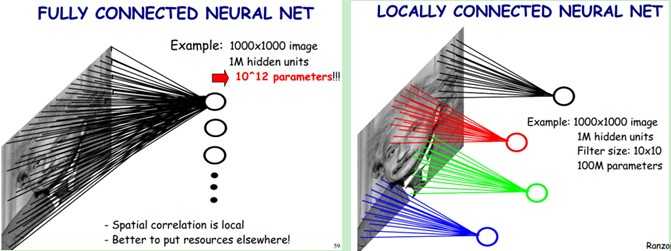
传统的神经网络的参数量是非常巨大的，比如1000X1000像素的图片，映射到和自己相同的大小，需要（1000X1000）的平方，也就是10的12次方，参数量太大了，而CNN除全连接层外，卷积层的参数完全取决于滤波器的设置大小，比如10x10的滤波器，这样只有100个参数，当然滤波器的个数不止一个，也就是下面要说的多卷积核。但与传统的神经网络相比，参数量小，计算量小。整个图片共享一组滤波器的参数。

3.3 多卷积核

一种卷积核代表的是一种特征，为获得更多不同的特征集合，卷积层会有多个卷积核，生成不同的特征，这也是为什么卷积后的图片的高，每一个图片代表不同的特征。

4. CNN实现架构

这里以LeNet-5(效果和paper)为例，一个典型的用来识别数字的卷积网络，当年美国大多数银行就是用它来识别支票上面的手写数字的。能够达到这种商用的地步，它的准确性可想而知。

LeNet-5主要有7层（不包括输入和输出），具体框架如图

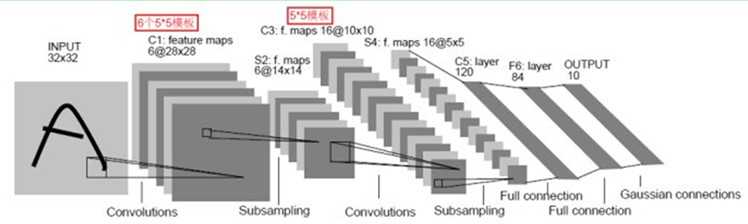
流程：输入层——>第一层卷积层——>第一层池化层——>第二层卷积层——>第二层池化层——>三层全连通层——>输出层

详解：输入是一个2维的图片，大小32X32，经过第一层卷积层，得到了C1层的6个28X28的特征映射图，6个说明了第一层卷积层用了6个卷积核。这里卷积后大小变成28X28，这是因为卷积有两种，一种有填充，卷积后与原图像大小一样，另一种不带填充，卷积后结果与原图像相比，小了一些。然后经过第一层池化层，28X28变成了14X14，一般是每邻域四个像素中的最大值变为一个像素，相应图片的长和宽各缩小两倍。然后又经过一个卷积层，变成了C3层的16个10X10的特征映射图，然后又经过一个池化层，得到S4层的16个5X5的特征映射，然后将这16个5X5的特征映射送到3层的常规神经网络，得出最后的结果。

总结：我们可以这样想，前面的卷积层和池化层是为了提取输入的高级特征，送到全连通层的输入，然后训练出最后的结果。

5.dropout

dropout是一种正则化的方法，应用在CNN中，主要解决CNN过拟合的问题。

怎么理解这个东西呢，首先我们要知道为什么过拟合？这是因为神经网络的神经元过多，参数过多，导致训练集拟合得太好了，为此，我们想dropout(丢掉)一些神经元，让它不产生影响。

具体做法:在每个隐藏层的输入进行一个概率判决，比如我们设置概率为0.5（通常命名为keep_drop）,根据0.5，我们生成一个跟隐藏层神经元个数的向量，true:false的比例是1：1（因为keep_drop=0.5），与隐藏层的输入进行相乘，那么会有一半隐藏层的神经元被丢掉，不起作用，整个网络变得简单了，就会从过拟合过渡到just right 。这是组合派的说法，andrew也是这么讲的，文末链接中还有一派噪声派的说法，也很有意思，可以看看！

6.结尾

CNN初探到此结束，当然，这是一个非常强大的算法，还需细细思考，体会其中更精华的东西！最后，由于笔者能力有限，如果错误，还请不吝指教！

在这里说一句，吴恩达的deeplearning.ai正式在网易云上线，全免费，非常值得观看哦！点开链接即可观看！

参考

[1] https://en.wikipedia.org/wiki/Convolutional_neural_network

[2] http://blog.csdn.net/zouxy09/article/details/8781543

[3] http://dataunion.org/11692.html

[4] http://blog.csdn.net/stdcoutzyx/article/details/49022443

CNN详解

标签：函数   cti   深度学习   解决   数据处理   tar   ann   不为   out   

原文地址：http://www.cnblogs.com/fydeblog/p/7450413.html