（原创）Stanford Machine Learning (by Andrew NG) --- (week 7) Support Vector Machines

标签：style   blog   class   code   java   c   

本栏目内容来源于Andrew NG老师讲解的SVM部分，包括SVM的优化目标、最大判定边界、核函数、SVM使用方法、多分类问题等，Machine learning课程地址为：https://www.coursera.org/course/ml

大家对于支持向量机（SVM）可能会比较熟悉，是个强大且流行的算法，有时能解决一些复杂的非线性问题。我之前用过它的工具包libsvm来做情感分析的研究，感觉效果还不错。NG在进行SVM的讲解时也同样建议我们使用此类的工具来运用SVM。 

（一）优化目标（Optimization objective）

首先回顾一下逻辑回归(logistic regression)：

objective function：        

Decision boundary：

• if y = 1，we want h_θ(x) ≈ 1 即  θ^Tx ? 0
• if y = 0，we want h_θ(x) ≈ 0 即  θ^Tx ? 0

Cost Function：

Goal：   Min J(θ) 

其中J(θ)中的log项如下图中的蓝色曲线所示，可见该部分始终≠0。而对于SVM，我们使用紫色折线所示的分段的折线作为代价函数（cost function中的log部分）。

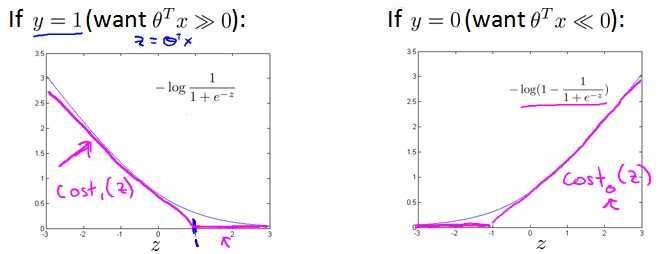
SVM的cost Function：

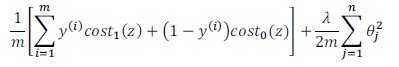
为最小化J(θ)，理想中令J(θ)→0，那么：

• if y = 1，对于cost₁(z)，when z ≥ 1，cost₁(z) = 0；
• if y = 0，对于cost₀(z)，when z ≤ -1，cost₁(z) = 0；

调整SVM的cost Function：

• 去掉1/m（对最优化结果不影响）；
• 令C = 1/λ，使得cost function中的正则项主要控制代价函数(J(θ)左部分)部分；

调整后SVM的cost Function：

 PS：调整后的J(θ)是一个凸函数(convex function)，故求解时不会陷入局部最优。 

（二）SVM最大判定边界(Large Margin Classifier)

假设C取一个很大的值，为Min J(θ)，就要求J(θ)中左边的部分尽量小，理想中→0，那么：

• y=1时，令Cost₁(θ^Tx)=0，即θ^Tx ≥ 1（not just ≥ 0）；
• y=0时，令Cost₀(θ^Tx)=0，即θ^Tx ≤ -1（not just < 0）；

decision boundary：

definition：能将所有样本点很好分类的h(x)边界，由于SVM可以找到一个与样本点之间有最大间隔的判定边界，故也叫做最大间隔分类器(Large Margin Classifier)。

例如，对于下图所示的分类问题，绿色、紫色和黑色直线都可以作为分类boundary，SVM就是尝试找到黑色直线这样的boundary，它距两个类相对较远。

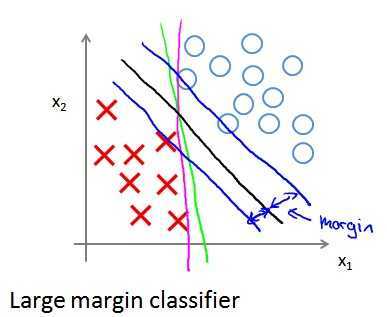
C对boundary的影响：

假设我们的样本点分布如下图所示：

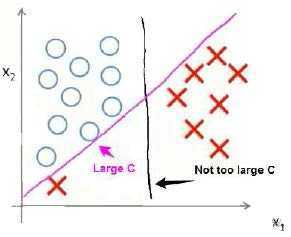
若data中存在一个明显的异常值，若C较大，SVM的判定边界为紫色直线；若C较小，SVM的判定边界为黑色直线。所以，我们可以的到结论：C值越小，SVM对异常数据越不敏感。

可以看出，C的取值可以在分类是否犯错和margin的大小上做一个平衡。  

（三）SVM形成Large Margin 的数学原因

从上一节中可以看出，当C较大时，会形成Large Margin Classification。

有人可能会问“为什么SVM是Large Margin Classification？”，下面就从数学的角度来解释。

1.向量内积(inner product)

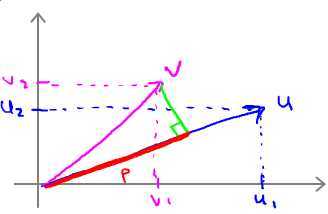
假设向量u、v是二维向量，那么u·v=u^Tv=u₁v₁+u₂v₂。在坐标系上表现为：将v投影到u上，其投影长度为p(u、v同向则p>0，反向则p<0)，即u·v=u^Tv=||u||·||v||·cosθ = ||u||·p = u₁v₁+u₂v₂。其中 ||u|| = sqrt(u₁²+u₂²)。

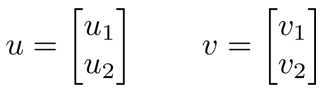
2.SVM Decision Boundary

回到之前的问题，“为什么选用较大的C会得到Large Margin Classification?”，当C较大，Min J(θ)时，要求J(θ)→0，那么 J(θ)只剩下右边的θ求和部分，现假设θ₀=0，只剩下θ₁和θ₂:

Goal：

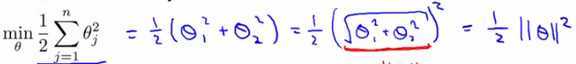
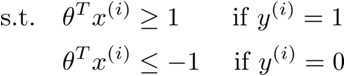
由于θ^Tx⁽ⁱ⁾ = p⁽ⁱ⁾·||θ|| = θ₁x₁⁽ⁱ⁾ + θ₂x₂⁽ⁱ⁾，p是x在θ上的投影，则cost Function的边界改为：

• y=1时，要求Cost₁(θ^Tx)=0，那么p·||θ|| ≥ 1
• y=0时，令Cost₀(θ^Tx)=0，那么p·||θ|| ≤ -1

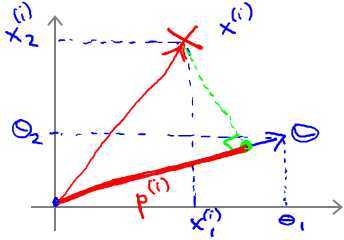
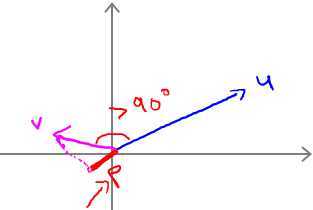
那么对下图所示的data set，绿色直线表示decision boundary，蓝色线表示θ向量。紫色为样本点在θ上面的投影。

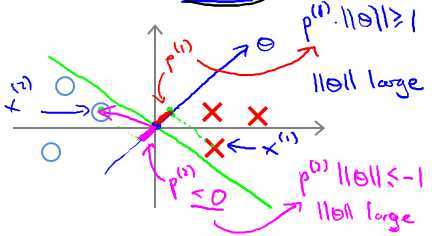
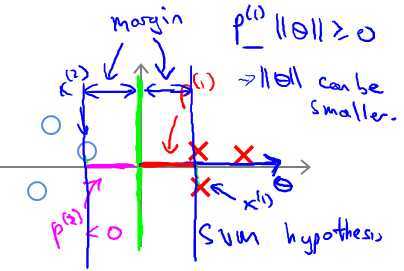
已知 boundary与θ向量呈90°.对于左边图所示的decision boundary，可见样本点在θ上面的投影非常小，即P很小，因此很难满足（y=1时，p·||θ|| ≥ 1；y=0时，p·||θ|| ≤ -1）的条件。因为，在p很小的情况下，只能使||θ||很大，这样就违背了 min 1/2*||θ||²，故这不是SVM得到的 boundary。同理，右边这个图中的 boundary就是比较好的，两边的数据在θ上面的投影都很大，这样||θ||就可以很小，这样按照cost Function求解就可以得到有large margin的 boundary了。

（四）核函数（Kernels）

在之前的学习中，我们知道对于非线性的问题我们可以通过构造多项式来拟合Decision boundary。

为得到上图中的边界，我们的模型可能是θ₀+θ₁x₁+θ₂x₂+θ₃x₁x₂+θ₄x₁²+θ₅x₂²+...，用新特征f来替换模型中的项，如f₁=x₁,f₂=x₂,f₃=x₁x₂,f₄=x₁²,f₅=x₂²,...,那么h_θ(x)=f₁+f₂+...+f_n。除了对特征进行组合之外，还有没有其他的方法构造f₁,f₂,f₃么？

给定样本x，计算x与我们预先选定的地标（landmarks）l⁽¹⁾,l⁽²⁾,l⁽³⁾的近似度作为特征f₁,f₂,f₃。

eg：

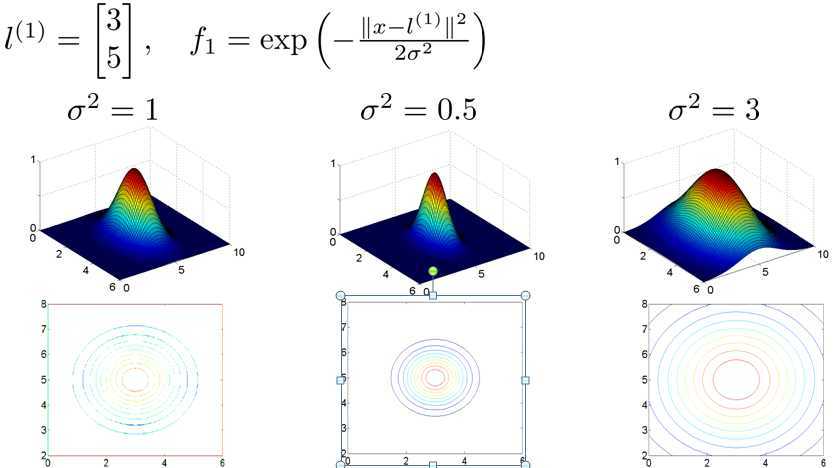
其中||x-l⁽¹⁾||² 是x的所有特征与地标l⁽¹⁾之间的距离之和，similarity(x,l⁽¹⁾)是高斯核函数(Gaussian Kernel)。

• if x 距离 l⁽¹⁾很近，那么f₁≈e⁰ ≈ 1；
• if x距离l⁽¹⁾很远，那么f₁≈e^{-(large number)} ≈ 0；

现假设训练集样本有两个特征x₁,x₂，给定地标l⁽¹⁾和σ值。下图中水平面坐标为x₁,x₂,垂直坐标为f。因此当x与l⁽¹⁾重合时具有最大值。随x改变f的变化速率受σ²影响。

SVM核函数的运用：

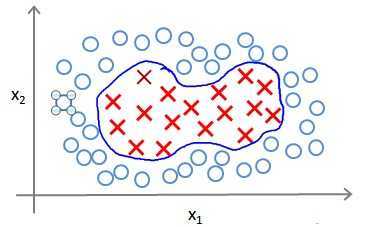
 如下图所示，当预测实例x处于紫色点位置，可以看出x离l⁽¹⁾较近，离l⁽²⁾,l⁽³⁾较远，故f₁≈1，f₂,f₃≈0。因此h_θ(x)=θ₀+θ₁f₁+θ₂f₂+θ₃f₃>0，预测y=1。同理当预测实例x处于绿色点位置，也预测y=1。若预测实例x处于蓝色点位置，可见x离l⁽¹⁾,l⁽²⁾,l⁽³⁾三个地标都较远，预测y=0。

这样，图中红色的曲线便是我们依据训练实例和地标得到的判定边界。

PS：预测时，我们采用的特征并非训练实例本身，而是通过核函数计算出的新特征f₁,f₂,f₃。

Landmark的选择：

通常，我们根据data set的数量来选择地标的数量。即若data set中有m个样本，则选取m个landmark。且令l⁽¹⁾=x⁽¹⁾,l⁽²⁾=x⁽²⁾,...,l^(m)=x^(m)。那么对于训练样本x⁽ⁱ⁾：

• f0(i) = 1
• f1(i)=similarity(x(i),l(1))
• f2(i)=similarity(x(i),l(2))
• ...
• fi(i)=similarity(x(i),l(i)) = similarity(x(i),x(i))=1
• ...
• fm(i)=similarity(x(i),l(m))

SVM的使用步骤：

objective function：给定x，计算x的新特征f，若θ^Tf ≥ 0，预测y=1。否则y=0.

cost function：      

有人会问：“为什么在逻辑回归中没有使用核函数呢？”其实在逻辑回归中我们也可以使用核函数，但是计算会非常耗时。

其他核函数：

以下这些核函数的目标也是根据training set和landmarks之间的距离来创建新的特征，这些核函数要满足Mercer‘s定理。

• 多项式核函数（Polynomial Kernel）

• 字符串核函数（String kernel）

• 卡方核函数（ chi-square kernel）

• 直方图交集核函数（histogram intersection kernel） 

（五）SVM的使用

我们在这里不介绍SVM Min J(θ)的方法，可以使用软件包(libsvm,liblinear等)。在使用这些软件包时，我们通常需要选择适当的核函数和C参数。

PS：

• 若使用高斯核函数，在使用前需对数据进行缩放。
• 如果我们不采用复杂的函数或training set特征多而样本数较少时，也可以不使用核函数(或linear kernel)的SVM。

C和σ²对SVM的影响：

• C较大（λ较小）时，可能会过拟合（Low bias, high variance）；
• C较小（λ较大）时，可能会欠拟合（High bias, low variance）；
• σ²较大时，High bias, low variance；
• σ²较小时，Low bias, high variance； 

（六）多分类问题（Multi-class classification）

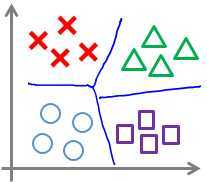
可使用one-vs.-all 方法：类似雨之前讲的逻辑回归的多分类问题的解决，对于k个类，需要训练k个模型，得到k个参数向量θ，选择θ^Tx的最大值对应的分类。实际上，很多软件包都有内置的多分类功能，可以直接使用。

（七）逻辑回归 vs. SVM

n: number of features ;
m: number of training examples;

PS：神经网络在上述三种情况下都有很好的表现，但是训练神经网络可能会非常慢。

HOMEWORK

好了，既然看完了视频课程，就来做一下作业吧，下面是Support Vector Machines部分作业的核心代码：

1.gaussianKernel.m

sim=exp(-sum((x1-x2).^2)/(2*sigma^2));

2.dataset3Params.m

 1 step = [0.01,0.03,0.1,0.3,1,3,10,30];
 2 J = zeros(length(step));
 3 for i = 1:length(step)
 4     for j = 1:length(step)
 5         C = step(i);
 6     sigma = step(j);
 7         model = svmTrain(X,y,C,@(x1,x2)gaussianKernel(x1,x2,sigma));
 8         predict = svmPredict(model,Xval);
 9         J(i,j) = mean(double(predict ~= yval));
10      end
11 end
12 
13 min_c=1;
14 min_s=1;
15 for i=1:length(step)
16   for j=1:length(step)
17     if J(i,j)<J(min_c,min_s)
18       min_c=i;
19       min_s=j;
20     end
21   end
22 end
23 
24 C=step(min_c);
25 sigma=step(min_s);

3.processEmail.m

1 for i=1:length(vocabList)
2     temp = strcmp(str,vocabList{i});
3     if temp == 1
4        word_indices = [word_indices;i];
5     end
6 end;

4.emailFeatures.m

（原创）Stanford Machine Learning (by Andrew NG) --- (week 7) Support Vector Machines,布布扣,bubuko.com

（原创）Stanford Machine Learning (by Andrew NG) --- (week 7) Support Vector Machines

标签：style   blog   class   code   java   c   

原文地址：http://www.cnblogs.com/tec-vegetables/p/3698993.html