球体与简单几何体的切接问题

标签：简单   http   src   inf   class   math   切面   固定   分享   

球体与正方体

• 棱长为\(a\)的正方体，其面对角线长为\(\sqrt{2}a\)；体对角线长为\(\sqrt{3}a\)；

• 棱长、面对角线、体对角线三者之比为\(1：\sqrt{2}：\sqrt{3}\)；

• 正方体的内切球的半径\(r_{内}=\cfrac{a}{2}=OF\)；

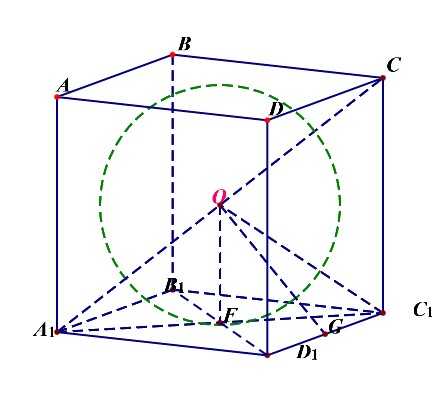
正方体与各条棱相切的球的半径\(R_{棱}=\cfrac{\sqrt{2}a}{2}=OG\)；

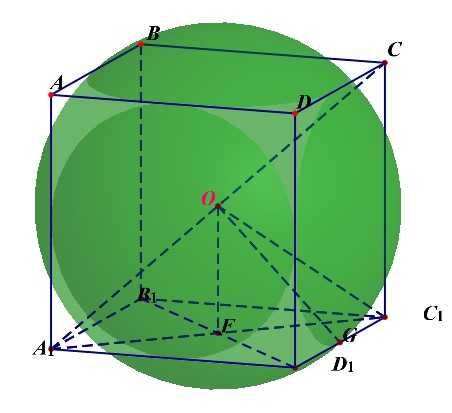
正方体的外接球的半径\(R_{外}=\cfrac{\sqrt{3}a}{2}=OC_1\)；

• 切面球半径\(r_{内}\)、切棱球半径\(R_{棱}\)、切点球半径\(R_{外}\)三者之比为\(1：\sqrt{2}：\sqrt{3}\)；

球体与正方体

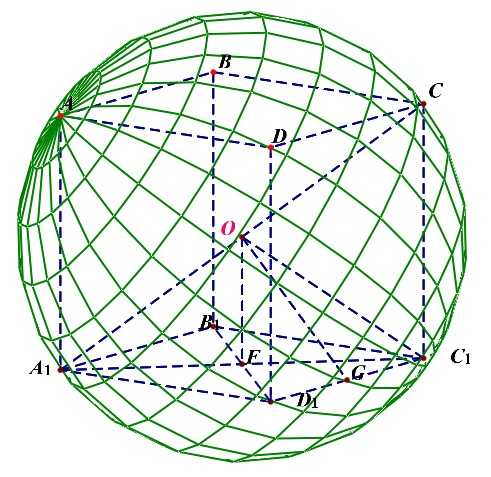
• 长方体的长\(a\)宽\(b\)高\(c\)，其面对角线的长不是固定的，其体对角线的长为\(\sqrt{a^2+b^2+c^2}\)；

• 长方体必有外接球，其半径\(R_{外}=\cfrac{\sqrt{a^2+b^2+c^2}}{2}\)；不一定有内切球；

球体与正四面体

• 正四面体的棱长为\(a\)，则其高为\(h=\cfrac{\sqrt{6}a}{3}\)；

• 正四面体的内切球半径\(R_{内}=\cfrac{\sqrt{6}a}{12}=\cfrac{1}{4}h=IF\)；

• 正四面体与各棱相切的球半径\(R_{棱}=\cfrac{\sqrt{2}a}{4}=IE\)；

• 正四面体的外接球半径\(R_{外}=\cfrac{\sqrt{6}a}{4}=IC\)；

球体与正三棱锥

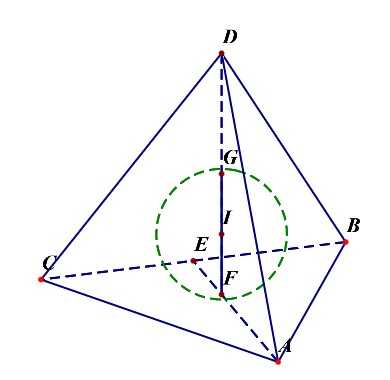
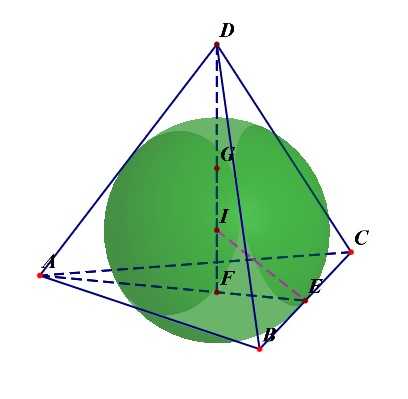
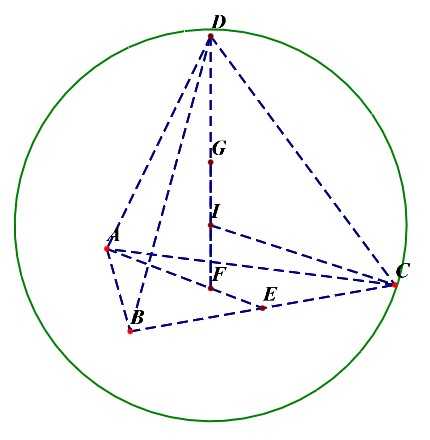
• 正三棱锥的棱长为\(a\)；则其高为\(h=\)；

• 正三棱锥的内切球半径；

• 正三棱锥的外接球半径；

例1一个正方体的顶点都在球面上，若这个球的体积是\(\cfrac{\sqrt{3}\pi}{2}\)，则正方体的棱长为___________.\(1\)

分析：设正方体的棱长为\(a\)，外接球的半径为\(R\)，则\(a^2+(\sqrt{2}a)^2=(2R)^2\)，

又\(\cfrac{4}{3}\pi R^3=\cfrac{\sqrt{3}\pi}{2}\)，即\(8R^3=3\sqrt{3}\)，

即\((2R)^3=3\sqrt{3}\)，两边同时\(\cfrac{2}{3}\)次方，得到

\((2R)^2=(3\sqrt{3})^{\frac{2}{3}}=3\)，

故有\(a^2+(\sqrt{2}a)^2=(2R)^2=3\)，解得\(a=1\)。

球体与简单几何体的切接问题

标签：简单   http   src   inf   class   math   切面   固定   分享   

原文地址：https://www.cnblogs.com/wanghai0666/p/10015765.html