标签:sig app 正态分布 require 维度 ldo shrink image 对比
众所周知,Robert Tibshirani是统计领域的大佬,这篇文章在1996年提出了LASSO,之后风靡整个高维领域,并延伸出许多种模型。这篇文章截止2019.5.16已经获得了27991的引用量(跪下)。
虽然LASSO是非常直观且大家都很熟悉的模型,但重温经典也无不可。了解一个模型就去读原作者的文章,获得的信息是最没有损失的。
在回归模型的场景中,我们使用最多的是最小二乘法估计参数(OLS)。
但OLS有很强的局限性,具体表现在:
预测精度(prediction accuracy)
OLS估计量出于最小化均方误差的目的,通常给出的估计结果有很低的偏差(拟合训练集的误差)但是有很高的方差(模型的泛化能力)
解释能力(interpretation)
保留大量的解释变量会降低模型的可解释性,因此需要找到一个具有很强影响力的解释变量子集。
为了解决上述问题,目前有两种方法:
subset selection
Cons:通过筛选变量增加了模型的解释能力。
Pron:但是模型并不稳健,因为选择变量是一个离散的过程,变量只会面临进入或退出两种可能。数据的微小改变会导致模型非常大的改变,因此降低预测的准确性。
ridge regression
Cons:是一个连续的变量系数缩减过程,因此较为稳定。
Pron:没有设置任何变量的系数为0,不能形成解释力强的模型。
基于此,作者提出LASSO模型,全称为‘least absolute shrinkage and selection operator‘(最小绝对收敛和选择算子),能够同时保留两种方法的优点。
一个类似的模型是Breiman于1993年提出的non-negative garotte.
\[
(\hat{\alpha},\hat{\beta})=\arg min{\sum_{i=1}^N(y_i-\alpha-\sum_jc_j\hat{\beta_j}^ox_{ij})^2}
\\subject \quad to\quad c_j\ge0\quad\sum_jc_j\le t
\]
个人感觉这个模型是通过允许缩减系数的存在但限制缩减系数的大小来实现对传统回归模型的优化。该模型相较subset selection能够减少预测误差,效果和ridge regression差不多。但该模型直接使用了OLS估计,如果OLS估计量本身表现差,那么这个模型也会表现差。
LASSO避免了对OLS估计量的直接使用。
接下来,作者以标准化的解释变量为例。set \(x^i=(x_{i1},\dots,x_{ip})^T\) ,where \(\sum_ix_{ij}/N=0,\sum_ix_{ij}^2/N=1\), i.e, \(X^T\cdot X=I\) .
参数向量\(\hat{\beta}=(\hat{\beta_1},\cdots,\hat{\beta_p})^T\),lasso估计量通过求解下列优化问题得到:
\[
(\hat{\alpha},\hat{\beta})=\arg min{\sum_{i=1}^N(y_i-\alpha-\sum_j\beta_jx_{ij})^2}
\\subject \quad to\quad \sum_j|{\beta_j}|\le t
\tag{1}
\]
同时假设\(\bar{y}=0\),因此可以省略\(\alpha\)。估计最优系数不需要设计矩阵是满秩的,这一点对于高维问题有很好的适应性。
方程(1)的解为
\[
\hat{\beta_j}=sign(\hat{\beta^0_j})(|\hat{\beta^0_j|}-\gamma)^+
\]
| Ridge Regression | Garotte Method |
|---|---|
| \(\frac{1}{1+\gamma}\hat{\beta_j^o}\) | \((1-\frac{\gamma}{\hat{\beta_j^{o2}}})^+\hat{\beta_j^o}\) |
接下来从图形上展示lasso方法,使用二维
空间p=2。由于lasso的限制条件是有棱角的,因此更容易切在某一维度的参数取零的点。
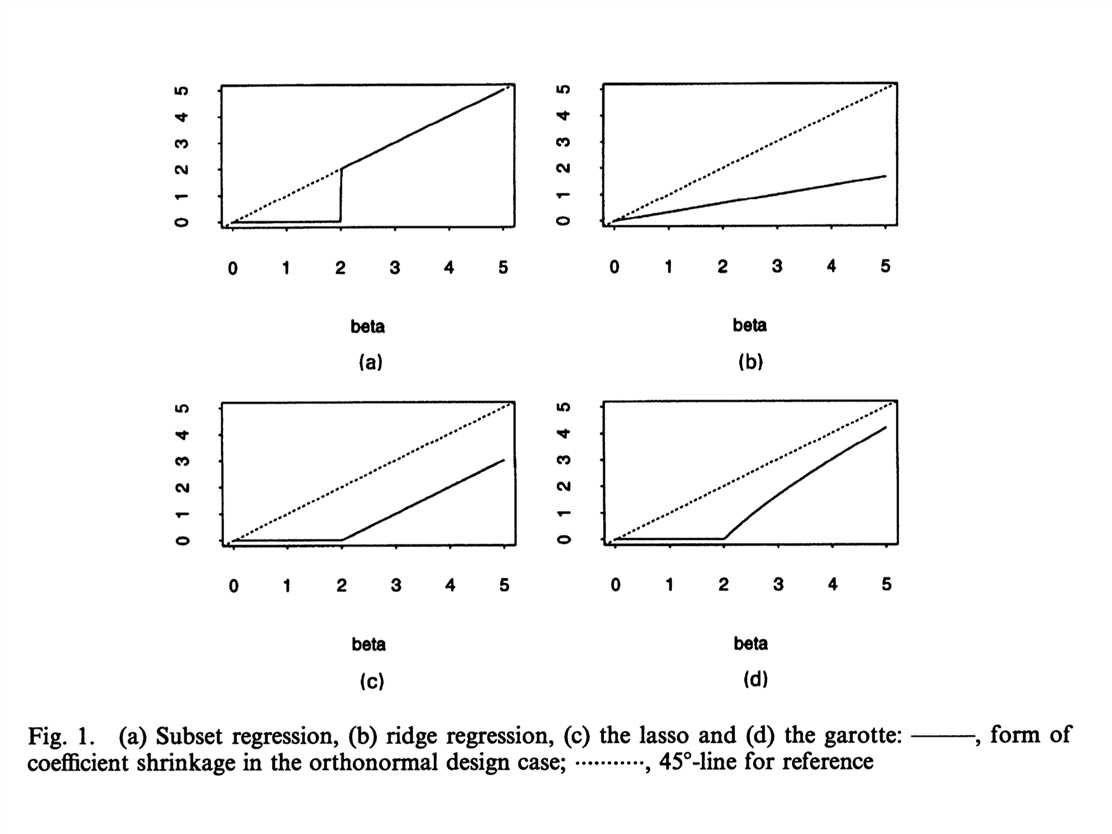
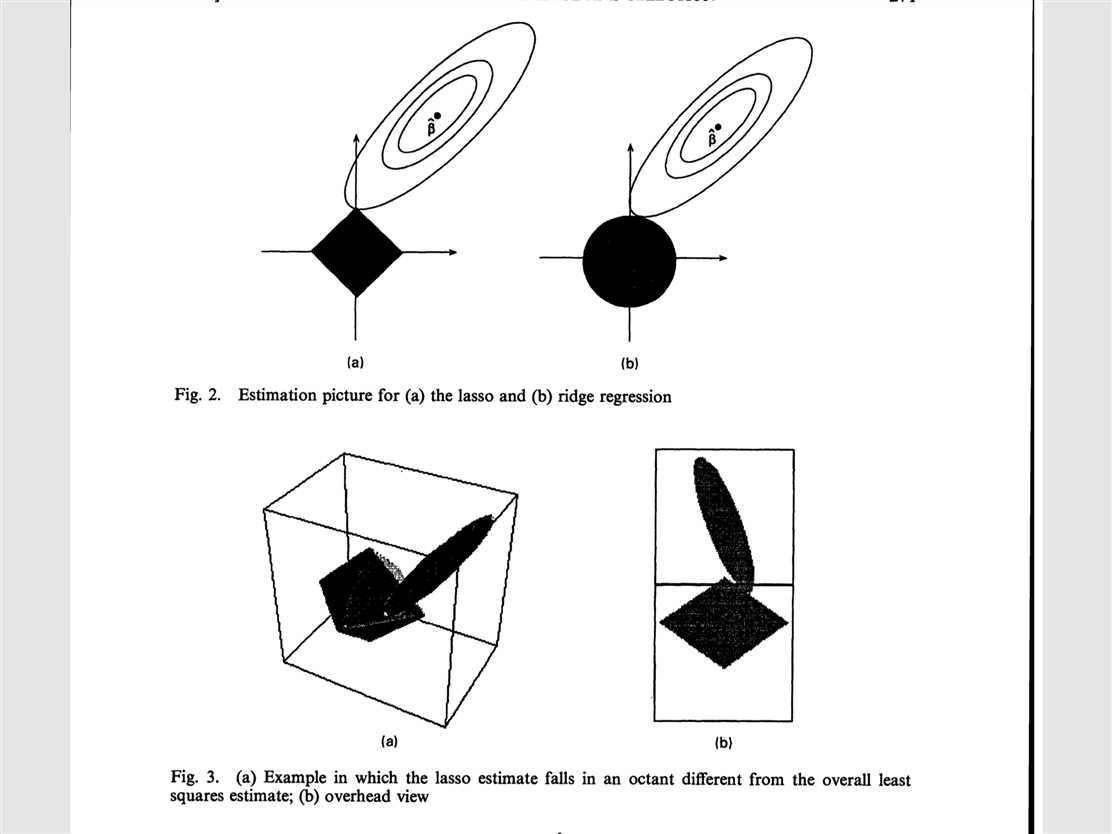
将变量个数拓展为两个后,对系数的估计结果为(不失一般性,假设OLS估计的系数为正):
\[
\begin{array}{c}{\hat{\beta}_{1}=\left(\frac{t}{2}+\frac{\hat{\beta}_{1}^{\circ}-\hat{\beta}_{2}^{\circ}}{2}\right)^{+}} \\ {\hat{\beta}_{2}=\left(\frac{t}{2}-\frac{\hat{\beta}_{1}^{\circ}-\hat{\beta}_{2}^{\circ}}{2}\right)^{+}}\end{array}
\]
系数的估计对变量之间的相关系数并不敏感。
然而,在二元情况下,岭回归的估计结果取决于变量之间的相关程度。当相关系数为0时,岭回归有缩减系数的效果,但随着变量的相关性增强,系数缩减效果越来越低,甚至在增加。(后面的simulation中可以看到)
As pointed out by Jerome Friedman, this is due to the tendency of ridge regression to try to make the coefficients equal to minimize their square norm.
首先将惩罚项写成\(\Sigma \beta_{j}^{2} /\left|\beta_{j}\right|\)的形式,然后借助岭回归来估计系数的协方差矩阵:
\[
\left(\mathbf{X}^{\mathrm{T}} \mathbf{X}+\lambda \mathbf{W}^{-}\right)^{-1} \mathbf{X}^{\mathrm{T}} \mathbf{X}\left(\mathbf{X}^{\mathrm{T}} \mathbf{X}+\lambda \mathbf{X}^{-}\right)^{-1} \hat{\boldsymbol{\sigma}}^{2}
\]
此外,还有一个通过迭代岭回归求解的方式,但在算法效率上较低。不过这一方式可以用于选择lasso parameter t。
| x (after standardized) |
|---|
| log(cancer volume) |
| log(prostate weight) |
| age |
| log(benign prostatic hyperplasia amount) |
| seminal vesicle invasion |
| log(capsular penetration) |
| Gleason score |
| percentage Gleason scores 4 or 5 |
需要预测的y为log(prostate specific antigen)【前列腺特定抗原】
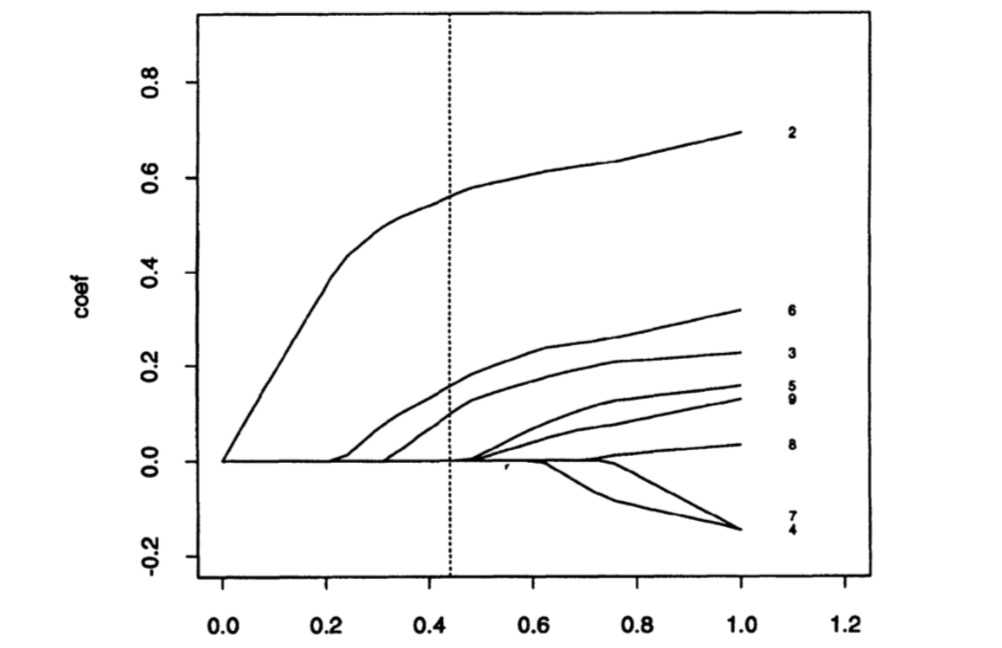
Lasso shrinkage of coefficients in the prostate cancer example: each curve represents a
coefficient (labelled on the right) as a function of the (scaled) lasso parameter \(s=t / \Sigma\left|\beta_{j}^{\circ}\right|\) (the intercept is not plotted); the broken line represents the model for \(\hat{s}\) = 0.44, selected by generalized cross-validation.
上图是设定了s的阈值后,各参数的缩减程度曲线。对于岭回归和subset regression,变量的选择不是单调的,即最后选出的5个最优变量和选出的4个最优变量不是包含关系。 \(\hat{s}\) = 0.44时,相当于我们只选择了一半的变量。
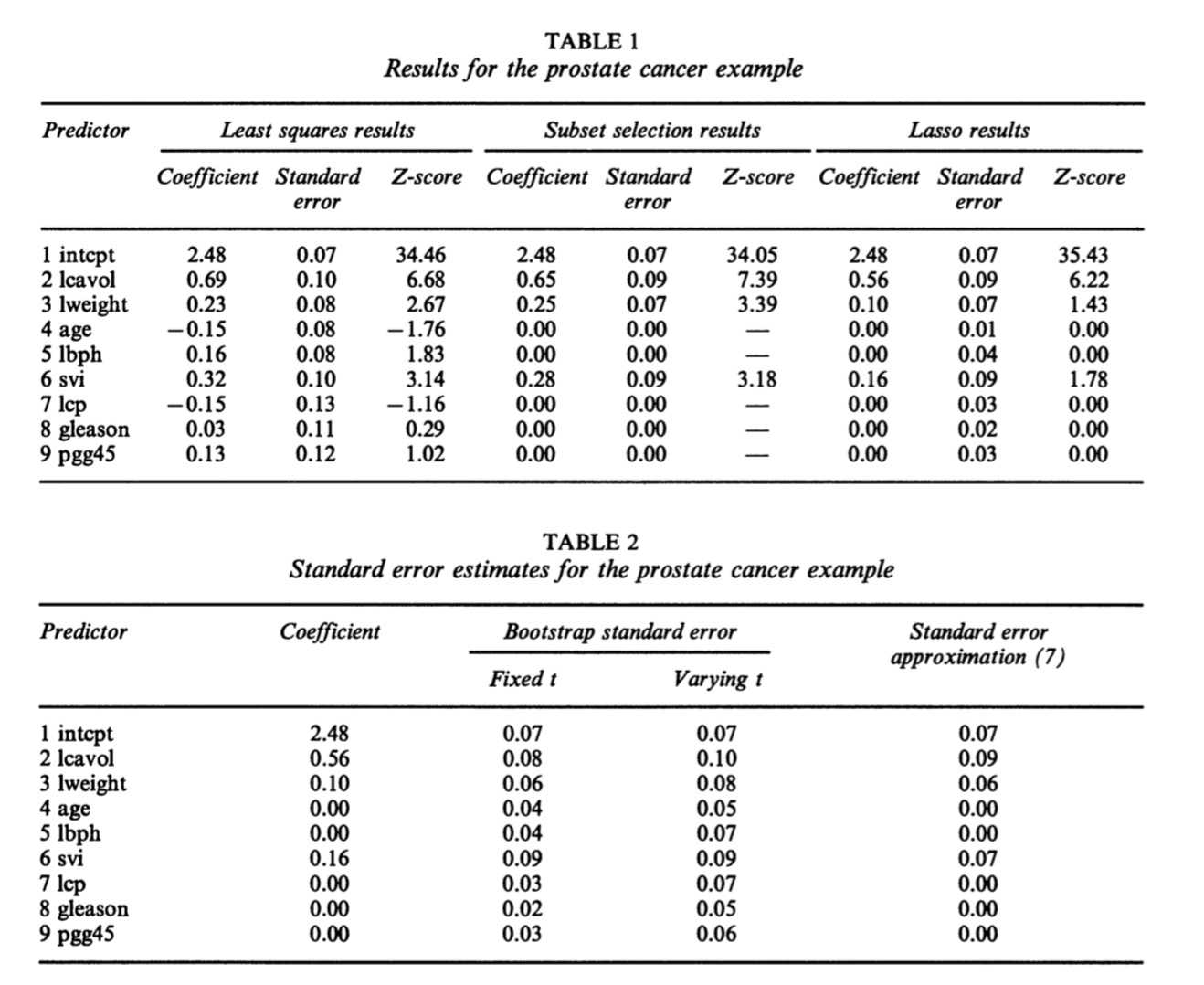
Notice that the coefficients and Z-scores for the selected predictors from subset selection tend to be larger than the full model values: this is common with positively correlated predictors. However, the lasso shows the opposite effect, as it shrinks the coefficients and Z-scores from their full model values.
对于subset selection,参数估计值通常要高于OLS估计(这种情况在变量有正相关时较为普遍)。但LASSO仍然能够保持缩减系数的效果。前面提到过,对于0系数标准差的估计,通过岭回归近似公式不能计算,但可以用bootstrap代替。
作者使用了三种方法估计lasso parameter:cross-validation, generalized cross-validation and an analytical unbiased estimate of risk。前两种适用于x为随机变量的情形,后一种适用于x固定的情形。在实际应用中,两种场景差别不大。
直接给出作者推导的结果。
1??通过交叉验证计算
给出PE(预测误差):
\[
\mathrm{PE}=E\{Y-\hat{\eta}(\mathbf{X})\}^{2}=\mathbf{M E}+\sigma^{2}
\]
作者采用了五折交叉验证,选出一个最优的\(\hat{s}\),使得PE最低。
2??通过lasso估计量的线性估计来推导t。(需要假设正交的design matrix)
\[
p(t)=\operatorname{tr}\left\{\mathbf{X}\left(\mathbf{X}^{\mathbf{T}} \mathbf{X}+\lambda \mathbf{W}^{-}\right)^{-1} \mathbf{X}^{\mathbf{T}}\right\}\\mathrm{GCV}(t)=\frac{1}{N} \frac{\mathrm{rss}(t)}{\{1-p(t) / N\}^{2}}\E_{\mu}\|\hat{\mu}-\mu\|^{2}=p+E_{\mu}\left(\|\mathbf{g}(\mathbf{z})\|^{2}+2 \sum_{1}^{p} \mathrm{d} g_{i} / \mathrm{d} z_{i}\right)\R\{\hat{\boldsymbol{\beta}}(\gamma)\} \approx \hat{\tau}^{2}\left\{p-2 \#\left(j ;\left|\hat{\beta}_{j}^{\circ} / \hat{\tau}\right|<\gamma\right)+\sum_{j=1}^{p} \max \left(\left|\hat{\beta}_{j}^{\circ} / \hat{\tau}\right|, \gamma\right)^{2}\right\}\\hat{\gamma}=\arg \min _{\gamma \geqslant 0}[R\{\hat{\boldsymbol{\beta}}(\gamma)\}]\\hat{t}=\sum\left(\left|\hat{\beta}_{j}^{\circ}\right|-\hat{\gamma}\right)^{+}
\]
第二种方法在计算效率上远胜第一种方法。generalized cross-validation介于上述两种方法之间。
当参数\(\beta_j\)具有独立双指数分布的先验假设时,也可以推导出LASSO估计量。由于指数分布的厚尾性质,可以在0点附近给更大的概率值。
Lawson and Hansen (1974) 提供了解决有不等式约束的线性最小二乘问题的方法。但对LASSO模型来说,\(m=2^p\)个约束条件太多了,实施起来很困难。但我们可以选择将不等式约束逐一加入,寻找满足KKT条件的解。
令\(g(\boldsymbol{\beta})=\boldsymbol{\Sigma}_{i=1}^{N}\left(y_{i}-\boldsymbol{\Sigma}_{j} \boldsymbol{\beta}_{j} \boldsymbol{x}_{i j}\right)^{2}\) ,将\(\Sigma\left|\beta_{j}\right| \leqslant t\) 拆成\(2^p\)个去掉绝对值的不等式约束\(\boldsymbol{\delta}_{i}^{\mathrm{T}} \boldsymbol{\beta} \leqslant t\)。
对于给定的\(\beta\),设置等式集E和不等式集S:\(E=\left\{i : \boldsymbol{\delta}_{i}^{\mathrm{T}} \boldsymbol{\beta}=t\right\} \text { and } S=\left\{i : \delta_{i}^{\mathrm{T}} \boldsymbol{\beta}<t\right\}\) .
\(\text { Denote by } G_{E} \text { the matrix whose rows are } \delta_{i} \text { for } i \in E\).
Algorithm outline:
(a) Start with \(E=\left\{i_{0}\right\}\)where \(\boldsymbol{\delta {i{0}}=\operatorname{sign}\left(\hat{\boldsymbol{\beta}}^{\circ}\right), \hat{\boldsymbol{\beta}}^{\circ}}\) being the overall least squares estimate.
(b) Find $ \hat{\beta}$ to minimize \(g(\boldsymbol{\beta})\)subject to \(G_{E} \boldsymbol{\beta} \leqslant t \mathbf{1}\).(1是1向量)#添加第一个不等式,求解
(c) While \(\left\{\Sigma\left|\hat{\beta}_{j}\right|>t\right\}\).#检查最终的条件
(d) add i to the set E where \(\boldsymbol{\delta}_{i}=\operatorname{sign}(\hat{\boldsymbol{\beta}})\). Find \(\hat{\beta}\) to minimize \(g(\boldsymbol{\beta})\)subject to
\(G_{E} \boldsymbol{\beta} \leqslant t \mathbf{1}\).#添加第二个不等式,并求解
该算法的收敛特性:
This procedure must always converge in a finite number of steps since one element
is added to the set E a t each step, and there is a total of 2p elements.The average number of iterations required is in the range (0.5p, 0.75p).
另一种完全不同的算法由David Gay提出。将原始问题转化为虽然具有2p个变量但限制条件减少为2p+1的问题。这种算法得到的解和原始问题的解一样。
\(\begin{array}{l}{\text { We write each } \beta_{j} \text { as } \beta_{j}^{+}-\beta_{j}^{-}, \text { where } \beta_{j}^{+} \text { and } \beta_{j}^{+} \text { are non-negative. Then we solve the }} \\ {\text { least squares problem with the constraints } \beta_{j}^{+} \geqslant 0, \beta_{j}^{-} \geqslant 0 \text { and } \Sigma \beta_{j}^{+}+\Sigma_{j} \beta_{j}^{-} \leqslant t . }\end{array}\)
标准的二次规划也可用于解决该问题,2p+1步内能保证收敛。
Standard quadratic programming techniques can be applied, with the convergence
assured in 2p +1 steps.
目的:比较普通最小二乘和lasso、non-negative garotte,best subset selection and ridge regression. 在每个case中都用五折验证法选择参数。
\[
\operatorname{PE}(J)=\frac{1}{5} \sum_{v=1}^{5} \operatorname{PE}^{v}(J)
\]
Zhang(1993) and Shao(1992)指出,如果只选择误差最小的模型,会导致估计的不一致性。
估计了50个data set,每个data set都包含20个观测值。
DGP为\(y=\boldsymbol{\beta}^{\mathrm{T}} \mathbf{x}+\sigma \epsilon\),where \(\boldsymbol{\beta}=(3,1.5,0,0,2,0,0,0)^{\mathrm{T}}\) and \(\epsilon\) 服从标准正态分布。变量之间的相关系数为\(\rho^{|i-j|}\),这里\(\rho\)设置为0.5,\(\sigma=3\).
这里可以看出,系数中有5个无意义。signal-to-noise ratio大约为5.7。
在200个模拟中,lasso效果最好,其次是garotte和岭回归。subset selection正确筛选掉了0系数,但是它的估计结果很不稳健。
同时,对比lasso和subset regression可以发现,虽然lasso完全估计出正确的模型(1,2,5)的频率很少,为2.5%,但它给出的模型包含正确参数的频率高达95%。而subset regression尽管给出完全正确模型的频率为24%,但所有模型中包含正确参数的频率仅为53.5%。
基本假设与example1一样,但是参数改为\(\beta_j=0.85\)。signal-to-noise ratio大约为1.8.最终结果显示LASSO和岭回归的在MSE意义上优于OLS,而其他几种方法效果都较差。LASSO的效果在这个example中不如岭回归,原因是DGP的参数不再包含0参数,而lasso倾向于筛选掉一些变量,因此相比岭回归存在更大的信息损失。
作者挑选了一个非常适合做subset selection的数据集,数据生成和example1一样,但设置\(\boldsymbol{\beta}=(5,0,0,0,0,0,0,0)\) ,\(\sigma=2\),因此signal-to-noise ratio大约为7.
结果显示garotte和subset selection效果最好,其次是lasso。岭回归的效果不佳,甚至不如OLS。
通过模拟一个更大的模型来检查lasso的表现。作者模拟了50个数据集,每个都有100个观测值和40个变量。DGP为:
\(x_{i j}=z_{i j}+z_{i} \text { where } z_{i j} \text { and } z_{i} \text { are independent standard normal variates. }\)
\(\boldsymbol{\beta}=(0,0, \ldots, 0,2,2, \ldots, 2,0,0, \ldots, 0,2,2, \ldots, 2)\),每个block重复了10次,\(\sigma=15\).
signal-to-noise ratio大约为9. 结果显示,岭回归效果最好,lasso其次。
IRLS: models a quadratic approximation to \(\ l (\beta)\) and leads to an iteratively reweighed least squares procedure for computation of \(\beta\) .和牛顿迭代原理一样。
使用驼背数据kyphosis data( analysed in Hastie and Tibshirani (1990))。
description:
0=absent,1=present。
x1=age,x2=number of vertebrae levels,x3=starting vertebrae level.
number of oberservations=83.
由于解释变量的影响不是线性的(可能影响越来越大or小,医学上的经验?)。作者还在模型中加入了二次项。变量都经过了标准化。
logistic regression:
\[
-2.64+0.83 x_{1}+0.77 x_{2}-2.28 x_{3}-1.55 x_{1}^{2}+0.03 x_{2}^{2}-1.17 x_{3}^{2}
\]
backward stepwise deletion:
\[
-2.64+0.84 x_{1}+0.80 x_{2}-2.28 x_{3}-1.54 x_{1}^{2}-1.16 x_{3}^{2}
\]
Lasso:
\[
-1.42+0.03 x_{1}+0.31 x_{2}-0.48 x_{3}-0.28 x_{1}^{2}
\]
大约5次后收敛。
lasso:\(\hat{\beta}_{j}=\operatorname{sign}\left(\hat{\beta}_{j}^{\circ}\right)\left(\left|\hat{\beta}_{j}^{\circ}\right|-\gamma\right)^{+}\)软阈值。
subset selection:\(\tilde{\beta}_{j}=\hat{\beta}_{j}^{\circ} I\left(\left|\hat{\beta}_{j}^{\circ}\right|>\gamma\right)\)硬阈值。
可以求出Risk的下界。
LASSO的优点:
另外提到lasso是bridge(使用了Lp正则)的特例。
标签:sig app 正态分布 require 维度 ldo shrink image 对比
原文地址:https://www.cnblogs.com/zzqingwenn/p/10874733.html