标签：密度   play   info   uri   概率论   href   www   class   code   

常见的分布

参考: https://www.cnblogs.com/pinking/p/7898313.html

1. 0-1分布

概率函数为:

\[P\{X=k\}=p^k(1-p)^k\] , 其中k取0或者1.

• 只有两种结果
• 试验只做一次

2. 几何分布

\(P(A)=p\) , 第\(k\)次首次发生,前\(k-1\)次未发生,概率函数为:

\[P\{X=k\}=p^k(1-p)^{k-1}\]

3. 二项分布

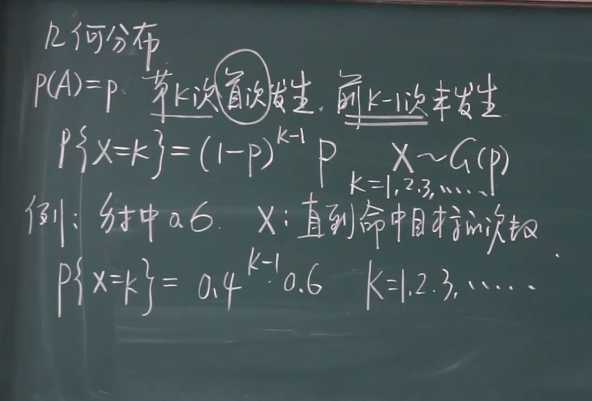
\(P(A)=p\), \(n\)次试验, 发生了\(k\)次, 概率函数为:

\[P\{X=k\}=C_n^kp^k(1-p)^{n-k}\]

• 二项分布最可能的值
• $如果(n+1)p为整数 , 那么最可能的值就是(n+1)p , (n+1)p-1 $
• \(如果(n+1)p不为整数 , 那么最可能的值就是[(n+1)p] 取整.\)

4. 泊松分布

概率函数为:

\[P\{X=k\}=\frac{\lambda^k}{k!}e^{-\lambda}, 其中\lambda >0, k=0,1,2,3,4,....\]

• 泊松分布的参数\(λ\)是单位时间(或单位面积)内随机事件的平均发生次数。 泊松分布适合于描述单位时间内随机事件发生的次数。
• 泊松分布的期望和方差均为\(λ\)

泊松分布与二项分布

当二项分布的n很大而p很小时，泊松分布可作为二项分布的近似，其中\(λ\)为\(np\)。通常当\(n≧20,p≦0.05\)时，就可以用泊松公式近似得计算。
事实上，泊松分布正是由二项分布推导而来的.

5. 超几何分布

定义如下:

例题:

6. 均匀分布

在概率论和统计学中，均匀分布也叫矩形分布，它是对称概率分布，在相同长度间隔的分布概率是等可能的。 均匀分布由两个参数a和b定义，它们是数轴上的最小值和最大值，通常缩写为\(U（a，b）\)。

其概率密度函数为:

\[p(x)=\frac{1}{b-a}, a\leq x \leq b \]
\[p(x)=0, else\]

7. 指数分布

• \(f(x)=\lambda e^{-\lambda x}\) , x>0, \lambda >0
• \(f(x)=0, x\leq 0\)
• \(E = \frac{1}{\lambda}\)

8. 正太分布

\[f(x)=\frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(x-\mu)^2}{2\sigma^2})\]

11- 常见的分布

标签：密度   play   info   uri   概率论   href   www   class   code   

原文地址：https://www.cnblogs.com/GGTomato/p/11831216.html