标签:mat sample dea which linear accept trie uitable nec
By R?za Özçelik
Original post: https://towardsdatascience.com/an-intuitive-explanation-of-graphsage-6df9437ee64f
DeepWalk is a transductive algorithm, meaning that, it needs the whole graph to be available to learn the embedding of a node. Thus, when a new node is added to existing ones, it needs to be rerun to generate an embedding for the newcomer.
In this story, we introduce GraphSAGE[1], a representation learning technique suitable for dynamic graphs. GraphSAGE is capable of predicting embedding of a new node, without requiring a re-training procedure. To do so, GraphSAGE learns aggregator functions that can induce the embedding of a new node given its features and neighborhood. This is called inductive learning.
We can divide GraphSAGE into three main parts as context construction, information aggregation, and loss function. Below we describe each part separately.
Similar to word2vec and DeepWalk, GraphSAGE also has a context-based similarity assumption.
GraphSAGE assumes that nodes that reside in the same neighborhood should have similar embeddings.
Similar to DeepWalk, the definition of the context is parametric. The algorithm has a parameter K that controls the neighborhood depth. If K is 1, only the adjacent nodes are accepted as similar. If K is 2, the nodes at distance 2 are seen in the same neighborhood as well.
Remark that having k = 2 means nodes at distance 4 can affect each other’s embeddings through the node in the middle. Therefore, increasing the walk length can introduce undesired information sharing between nodes. having a too large K can even cause having the same embedding for all nodes!
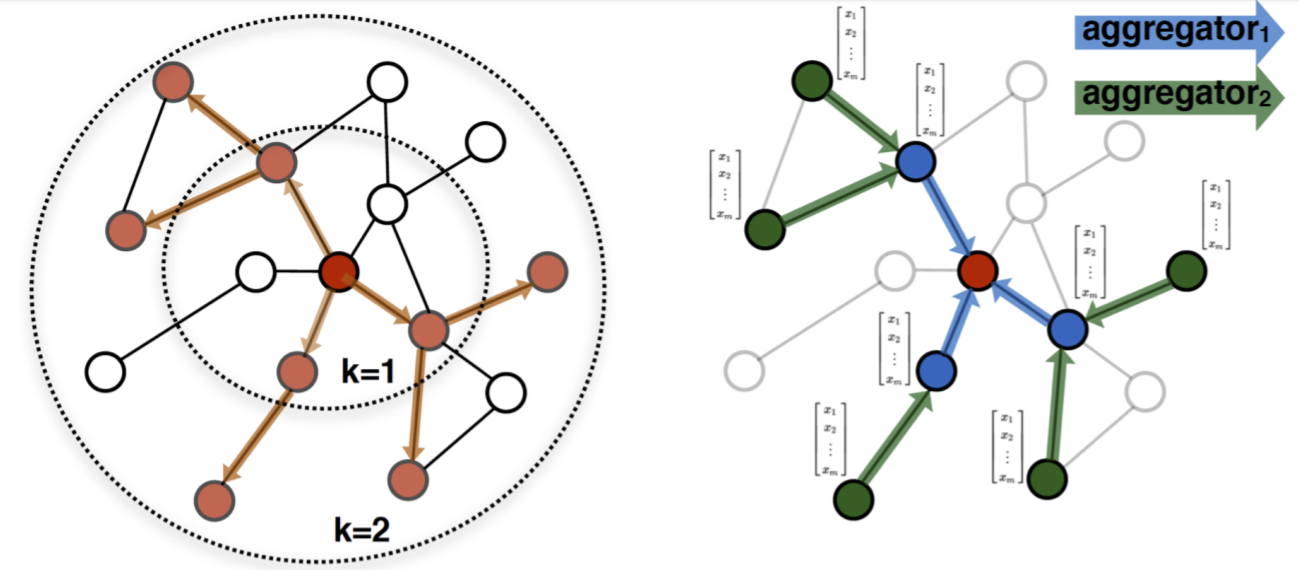
Neighborhood exploration and information sharing in GraphSAGE. [1]
Having defined the neighborhood, now we need an information sharing procedure between neighbors. Aggregation functions or aggregators accept a neighborhood as input and combine each neighbor’s embedding with weights to create a neighborhood embedding. In other words, they aggregate information from the node’s neighborhood. Aggregator weights are either learned or fixed depending on the function.
To learn embeddings with aggregators, we first initialize embeddings of all nodes to node features. In turn, for each neighborhood depth until K, we create a neighborhood embedding with the aggregator function for each node and concatenate it with the existing embedding of the node. We pass the concatenated vector through a neural network layer to update the node embedding. When each node is processed, we normalize the embeddings to have unit norm. The pseudo-code can be found below.

Pseudocode of GraphSAGE algorithm. [1]
The advantage of learning aggregator functions to generate node embeddings, instead of learning the embeddings themselves, is inductivity.
When the aggregator weights are learned, the embedding of an unseen node can be generated from its features and neighborhood.
As a result, aggregators remove the necessity of re-training when new nodes are introduced to the graph. Note that this is quite common in social networks, web, citation networks and so on.
Until now, we have described a procedure to generate node embeddings. Yet, to learn the weights of aggregators and the embeddings, we need a differentiable loss function. Based on our intuition, we want neighboring nodes to have similar embeddings and independent nodes to have distant embedding vectors. The function below satisfies these two conditions with two terms.
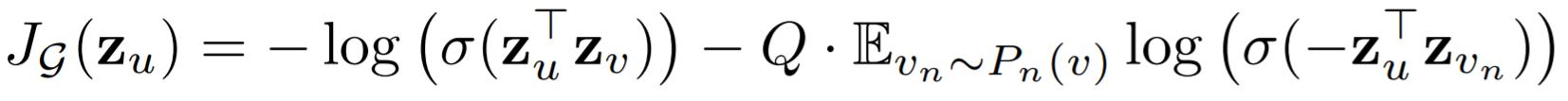
Loss function of GraphSAGE. [1]
Here u and v are two neighbors and the loss computed for u. The first term promotes maximizing the similarity of embeddings of u and v as we desired. In the second term, we have a variable Q, which is is the number of negative samples and v? is a negative sample drawn from negative sample distribution. A negative sample in this context means a non-neighbor node. This term tries to set apart embeddings of these two nodes. Lastly, σ is used to denote the sigmoid function as usual.
Remark that this is an unsupervised loss function that can be minimized with no labels. To use GraphSAGE in a supervised context, we have two options. We can either learn node embeddings as the first step and then learn the mapping between embeddings and labels, or we can add a supervised loss term to loss function and adopt an end-to-end learning procedure. This flexibility is valuable.
GraphSAGE owes its inductivity to its aggregator functions. We can define various aggregators that are either parametric or nonparametric. As a non-parametric function, we can use simple averaging. It other words, we can average embeddings of all nodes in the neighborhood to construct the neighborhood embedding.
A parametric function could be an LSTM cell. Yet, LSTM cells are designed for sequential operations and have memories. Hence, the order that the neighbors are fed to LSTM affects the neighborhood embedding, though there is not an apparent order. To alleviate this, random permutations of the nodes can be fed to LSTM. The parameters of LSTM would be learned when minimizing the loss function.
Another learnable aggregator is a single layer neural network followed by a max-pooling operator. To do so, we pass each neighbor’s embedding from a non-linear layer and apply an element-wise max operation to their outcomes. In the paper, this function is shown as the most promising one based on the experiments.
Though more complex aggregators can be designed, simplicity is desired since aggregators affect training time drastically. An ideal aggregator should be simple, learnable and symmetric. In other words, it should learn how to aggregate neighbor embeddings and be indifferent to neighbor order, while not creating a huge training overhead.
GraphSAGE is an inductive representation learning algorithm that is especially useful for graphs that grow over time. It is much faster to create embeddings for new nodes with GraphSAGE compared to transductive techniques. Additionally, GraphSAGE does not compromise performance for speed. It was tested on three different datasets that entail node classification, node clustering and across graph generalization and outperformed the existing solutions.
Nowadays, there are extensions of GraphSAGE to heterogenous networks as well as novel inductive approaches. Yet, GraphSAGE adopted a pioneering and influential role in inductive graph representation learning.
[1] Hamilton, Will, Zhitao Ying, and Jure Leskovec. “Inductive representation learning on large graphs.” Advances in Neural Information Processing Systems. 2017.
An Intuitive Explanation of GraphSAGE
标签:mat sample dea which linear accept trie uitable nec
原文地址:https://www.cnblogs.com/jcleung/p/12257618.html